研究ノート
ド・ブロイ波の力学的解釈
2025.5.26
五十川晋一
|
 目的
目的
フランスの理論物理学者、ド・ブロイは1924年に学位を取得し、その中で物質波の概念を示した。
”万物は振動している” という主旨だが、彼が登場する前の物理学の課題は光の粒子と波動の二重性であった。
それを式で示す事が出来ない状況が続いていたが、彼の物質波とは、光だけでなく、どんな物質も粒子であると同時に
振動していると見なすという試みであった。
彼が示した式は以下である。
| ν = m・c2 / h ν:物質の振動数、m:質量、c:光速、h:プランク定数 |
(1.1) |
これは物質の振動数と質量は互いに比例する、という事になる。
振動現象は数学的には三角関数=正弦波を用いて記述できるが、力学的には質量と剛性という二つの物理特性が不可欠である。
一方、量子力学では電子を近似的光速まで加速して対象物質に衝突させた際に発現する素粒子の質量を求めている。
この質量はアインシュタインの特殊相対性理論で示される以下の式を用いてエネルギから逆算される。
| E = m・c2 E:エネルギ、m:質量、c:光速 |
(1.2) |
こうして求められる質量だが、2012年時点では15種類が確定している。
素粒子の質量の値は公開されているが、一部を除いて巾を持っている。
観測されるエネルギの値は実験を行う度に異なり、定まらない事が知られている。
ここで筆者は以下のような推論を行った。
・値が定まらないという事から、加速される電子は振動しているが正弦波では無い。
・万物は振動しているとする物質波の考え方を適応するならば、ド・ブロイ波は正弦波では無い。
本報では力学的な視点で机上実験を行い波形を観察すると共に、素粒子の質量=エネルギが定まらない理由を考察する。
実験は物理機能モデル手法により、粒子と波動の性質を併せ持つ物質を2連のバネとしてモデル化する。
物理機能モデル手法の詳細は補足資料に示した。
 もくじ
もくじ
●柔らかい物質について
●エネルギの印加について
●机上実験
・実験用モデル
・パラメータ
・試験条件
●結果
・線形系の振動波形
・非線形系の振動波形
・エネルギを印加した場合の様相
●考察
・ド・ブロイの物質波は正弦波では無い
・素粒子の質量に巾がある理由
・ランダムと非ランダム、確率論と非確率論
・柔性と力エネルギ
・量子力学と物理機能モデルの対比
●まとめ
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[1]
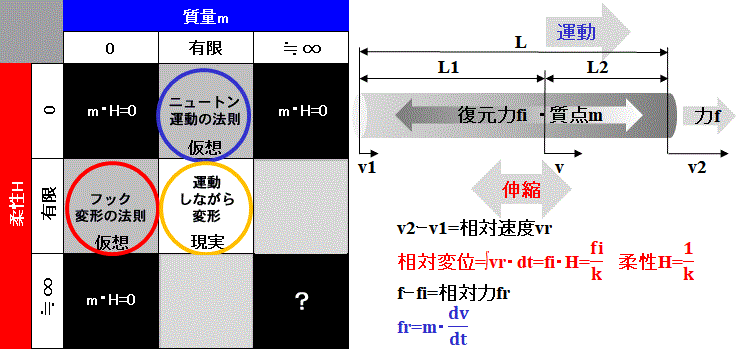
Fig.1
|
もくじへ戻る
 エネルギの印加について
エネルギの印加について
●エネルギ印加の事例
わかり易い事例をFig.2に示す。
水ヨーヨーはゴムひもの端を持って上下に振るが、振り方によって大きく振らす事が出来る。
水ヨーヨーの隣のバネは、同様に縁日で良く見かける玩具を示している。
このバネの元祖はSLINKYと呼ばれ、米国で1945年に玩具として登場し、その亜流が世界中に流布している。
SLINKYの遊び方は様々だが、水ヨーヨーと同じような遊び方が本報の例である。
遊びの中で無意識のうちに振るタイミングや周期を合わせている訳である。
逆にタイミングと周期を故意に合わせなければ、手を振ってもヨーヨーやバネを殆ど振らさない事も出来る。
エネルギの印加とは水ヨーヨーやバネ自身が蓄えているエネルギに対して外部から加えたり、逆に吸収する事であり、物質が励起される、去勢されると言う表現も出来る。
物質に蓄えられるエネルギEは以下のように定義される。
| Ev = 1/2 m・v2 Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.3) |
| Ef = 1/2 H・f2 Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.4) |
| E = Ev + Ef = const. |
(1.5) |
上式は力学の双対性を現し、式(1.5)は対になったエネルギの和は常に一定となる事からエネルギ保存則と呼べる。
補足資料1参照
|
●熱エネルギの印加
|
物質に蓄えられる熱エネルギEtは以下のように定義され、温度T(k)に依存する。
| Et = m・Cp・T Et:熱エネルギ、m:質量、Cp:比熱、T:温度 |
(1.6) |
これは物質を振動させる為のエネルギ源という見方である。
熱エネルギEtは同じ内包量*1である力エネルギEfに変換出来るので、Et = Ef = 1/2 H・f2 の関係から力fが求められる。
これは、熱エネルギと力エネルギが等価な物理量である事を意味している。 補足資料2参照
この力fを最初にバネに印加しておくことで、物質が熱エネルギを蓄えて振動している事を表現出来る。
なお、熱エネルギを印加すれば無重力下でも振動が起こる。
一方、重力下では熱エネルギEtを印加しなくとも重力が力fの代わりに振動のエネルギ源となる。
勿論、重力下で熱エネルギを印加しても良い。
*1:内包量については補足資料3参照
|
●振るタイミング
振るタイミングが振動している際の伸び側か、縮み側かで振れ方が異なり、波形は複雑である。
これは非線形力学系に見られる現象で、どのように振れるか=未だ観測していない未来の予測は困難だが、一度観測された結果は再現性が有り、決してランダムではないと言う性質を持っている。
例として、二重振り子のオモリが描くカオス軌道と呼ばれる複雑な軌跡が知られている。補足資料4参照
カオス軌道は数学的にフラクタルの性質と同じであり[2]、一度現れた軌跡は二度と重なる事が無い。 補足資料5参照
逆に正弦波だけで表現出来る線形力学系であれば規則性があるので、未だ観測していない未来の予測は可能
である。
線形力学系は現実界には存在しないが、工学の分野では課題に応じて実用上問題なければ線形系と見なして扱う事が慣例となっている。
|
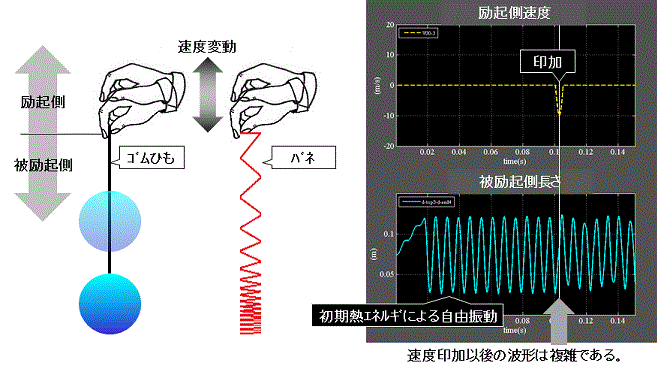
Fig.2
|
もくじへ戻る
 机上実験
机上実験
●実験用モデル
Fig.3_1に示すように、地球上でバネの一端を固定=垂直に吊るせば重力によって伸びる。
固定を解放すればバネは伸縮しながら落下する。 これが粒子と波動の性質を併せ持つと言う事である。[1]

Fig.3_1
Fig.3_2は物理機能モデルのモデル図である。
補足資料に示した基本モデルを2連にしたもので、物質の最小単位と言える。
2連である理由は、物質には長さがあり、左右に対の端部はお互いに独立した変位量を持つという事である。
1個のバネで表現出来る変位量とは、どちらか一端の速度を0=固定とした場合に限られる。
両端が解放されている場合、2連以上のバネでないと左右で独立した変位量が求められないからである。
バネ1個なら力学的に線形系だが、2連以上のバネは非線形系となる。
オモリが1個の振り子と2個の二重振り子も同じである。
課題に応じて3連、4連~n連でも良く、ひとつの物質をn要素に分割するという意味合いになる。
式(1.5)に示されるエネルギはn数に応じて整数比の値を取る。
これは1900年にプランクが示した黒体輻射の公式に含まれる性質と符合する。[3] [4]
|

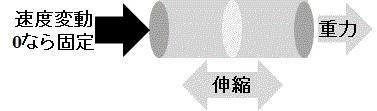
Fig.3_2
●パラメータ
・質量m:0.05(kg)×2
・柔性H:1.0e-5 (mN−1) ×2 (剛性kの逆数)
・粘性抵抗係数Cm:0(Nsm−1)
・塑性抵抗係数DH:0(ms−1 N−1)
・比熱Cp:449.5(JKg-1k-1) (鉄の比熱で代用)
・初期温度:5(k)=-ー268.15(℃)
・環境温度:5(k)=-ー268.15(℃)
・重力:0 無重力下とする
|
●試験条件
・サンプリング時間:1.0e−5(s)
・物質に熱エネルギを印加して振動させた後、既定の時刻に速度変動を印加する。
・速度変動周波数:100(s−1)
・速度変動振幅:10(ms−1)
・印加周期:半周期
・なお、物質は熱伝達の無い断熱条件下とする。
|
もくじへ戻る
 結果
結果
試験に先立ち、線形系と非線形系の違いを振動波形で示しておく。
●線形系の振動波形
線形系は正弦波であり、Fig.4は規則性がある事を可視化した図である。
使用しているモデルは基本モデルで、一端を固定して自由振動する1個のバネと考えて差し支えない。
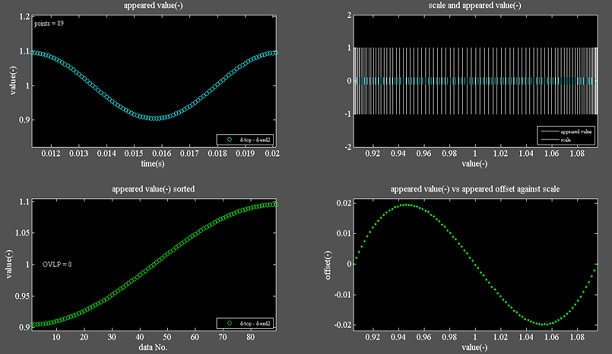
Fig.4
・左上図はX軸:時間、Y軸:バネの全長を89個のデータで示した1周期分の正弦波である。
・左下図は現れる全長の値をソートしたものである。
・右上図はX軸:全長に取り、バーコード様(白プロット)に表したものである。
・バーコードの間隔は規則的で左右対称である。
・水色プロットは全長の最大~最小をデータ数で分割して配置したもので、等間隔スケールである。
・右下図は各全長データについて等間隔スケールに対するオフセット量をY軸に取ったもので、点対称である。
|
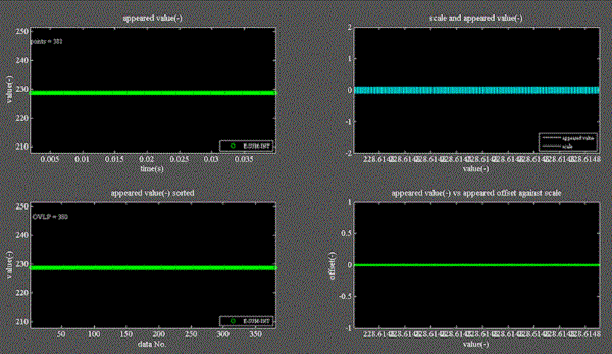
Fig.5
・バネが蓄えているエネルギを示す。
・左上図はX軸:時間、Y軸:エネルギであり、他はFig.4と同じ様式である。
・全長は変化するが、エネルギは式(1.5)に示されるように常に一定に保たれる。
|
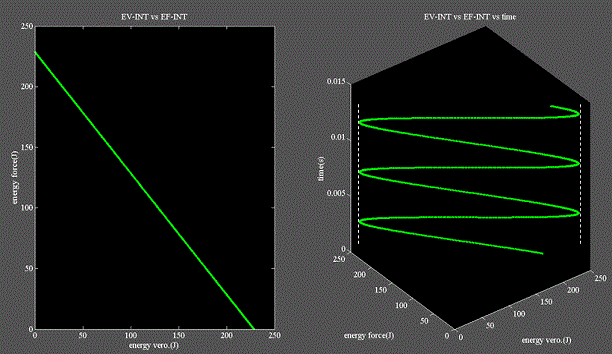
Fig.6
・左図はバネが蓄えているエネルギを速度エネルギと力エネルギに分離してXY座標上にプロットしたものである。
・時間の経過と共にプロットのXY座標の位置が変化する。
・すなわち、速度エネルギが増えれば同じ分だけ力エネルギが減る事を示している。
・言い方を変えると、こちらを立てればあちらが立たない=堂々巡り、モグラ叩きと言える。
・右図はそれを示す為にZ軸を時間軸とした3D表示である。
・ここでも速度エネルギと力エネルギの配分が正弦波様に変化している事が判る。
|
|
●非線形系の振動波形
|
線形系である1個のバネを2連にすると非線形系となり、全長は正弦波では無い事を示す。
|
●エネルギを印加した場合の様相
ここからが本試験の結果である。
Fig.10はFig.4、7と同じ様式で水ヨーヨーを振るように物質=バネの一端に速度を印加した後のエネルギの値を示す。
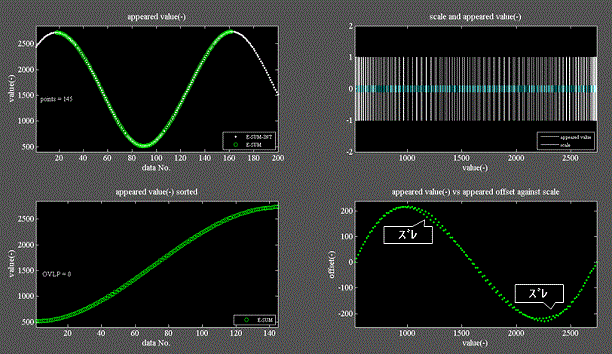
Fig.10
・左上図は印加タイミングをサンプリング時間毎にずらして200回繰り返した時のエネルギの値を試験順に並べたものである。時系列波形ではない事に注意。
・一見、規則性がある様に見えるが、そうではない事を可視化したものである。
・左下図はそのうちの1周期分に相当する145個のエネルギ値をソートしたものである。
・右上図のバーコードの間隔は不規則である。
・右下図にはズレが見られるので規則性が無い事が判る。
・物質に速度を印加する場合、そのタイミングによって蓄えるエネルギは定まらない事を示している。
|
|
もくじへ戻る
 考察
考察
●ド・ブロイの物質波は正弦波では無い
Fig.7で示したように、物質の全長は規則的な正弦波では無い。
正弦波にならない性質は非線形系の振動に現れるものである。
物理的な振動は数学の三角関数=正弦波を用いて記述出来る事から、様々な分野で物質を線形系として扱う事がある。
但し、物質を1個のバネでモデル化した場合にのみ線形系となり、2連以上では非線形系となる。
これは先述のように物質には長さがあり、左右に対の端部はお互いに独立した変位量を持つという事である。
1個のバネで表現出来る変位量とは、どちらか一端の速度を0=固定とした場合に限られる。
バネの一端が固定とは工学の分野ではバネの変位量を求める際に、便宜的にそれを固定している相手の物質を完全剛体と見なす事に相当する。
両端に速度を持つ=解放されている場合、2連以上のバネでないと左右に対となった各々の変位量が求められない。
机上実験に於いて一端に速度を印加している状況がこれに相当する。
また、物理学や工学上のいわゆるバネ・マス系とは、柔性はバネ、質量はマスに切り分けていると言える。
これは便宜上、伸縮はバネに任せ、マスは変形しない=完全剛体と見なすという事に他ならない。
一方、現実には完全剛体は存在せずバネにも質量があるゆえ、本来はバネとマスは切り分ける事が出来ない筈である。
従って、現実界に存在する物質は原子、電子と言った量子の段階から2連以上のバネであり、非線形系と言える。
よって、物質波は正弦波では無いと言える。
|
●素粒子の質量に巾がある理由
机上実験では物質に蓄えられるエネルギは温度に依存し、線形、非線形に関わらず常に一定に保たれる事を示した。
次に、物質=バネの一端に速度を印加する際、そのタイミングによって蓄えられるエネルギが異なる事を示した。
現実の電子自身の伸び~縮みは不確定性原理に阻まれて観測不可能ゆえ、速度を印加するタイミングは管理出来ずランダムとならざるを得ない。
衝突させる対象物質の伸び~縮みも同様ゆえ、衝突に際して観測されたエネルギは定まらないと言える。
素粒子の質量は観測されるエネルギの値から式(1.2)によって逆算されるゆえに定まらない。
|
●ランダムと非ランダム、確率論と非確率論
電子の加速~衝突実験はランダム実験とならざるを得ないが、机上実験ではサンプリング時間毎に速度印加のタイミングをずらしているので非ランダム実験と言える。
ここで、ランダム実験と非ランダム実験を比較すると、
・ランダム実験:定まらないエネルギ値の中からある値に絞り込むには、確率の概念を導入して統計分析が必要。
・非ランダム実験:結果は再現性があるので確率の概念は不要であり、絞り込む必要が無い。
Fig.7、10の左下図に示した観測値のソートは初歩的な統計処理だが、これだけでも段差やズレが現れる。
これが何かの兆候を示す訳ではないが、少なくとも物事が非線形系である事を示している。
量子力学では素粒子の波動を考える場合、確率波という概念を導入している。
先に非線形系に現れる性質としてフラクタルを挙げたが、重ならない、同じ値が出現しない、という性質がある。
これらは毛細血管や植物の枝分かれ、雪の結晶、リアス式海岸など、あらゆるところに現れる。 補足資料5参照
ランダムの中から重なる、同じ値が出現する確率を考えようとする立場はフラクタルとは噛み合わない。
一方フラクタルは数学上の性質であり、現実界では同じ値が出現する確率はゼロとは言い切れないと言う見方も出来る。*2
ここで2個の原子同士、又は2個の電子同士、あるいは1個の陽子と1個の電子を考える。
次にお互いが接近しうる限界距離を考えて見る。
人間同士がこれ以上詰められない距離=ソーシャルディスタンス=縄張りのようなものである。
例えば毛細血管の末端同士がその縄張りを侵略しないように自律的に細胞増殖を停止する仕組みがある筈である。
もし、それが停止できなければ末端同士は干渉し、その部分は腫瘍のように盛り上がってしまう。
この限界距離は最小分解能と言え、それ以下は同じ値と見なされると言う見方である。
言い方を変えると、現実界ではフラクタルの性質には打ち止めがあると言える。
この見方は研究ノート 電子の2重スリット実験に関する仮説にも出てくるので参考にされたい。
*2:量子力学に於けるベルの不等式の破れに関係する。
|
●柔性と力エネルギ
物理機能モデルでは物質を完全剛体とは見なさず、質量と柔性を持つ事を前提としている。
一方、量子力学では素粒子の質量は想定しているが、柔性を想定していない。
これは式(1.3)速度(運動)エネルギは想定しているが、式(1.4)力(変形)エネルギを想定していない事になる。
従って、式(1.5)で示したエネルギ保存則=力学の双対性が満たされていないと言える。
ただ、柔性を求めるには物質の長さと復元力を測らねばならず、不確定性原理に阻まれて求める事が出来ない。
そもそも伸縮しながら運動している物質の位置と長さは一意に定まらない。
物質の位置を左端とするのか右端とするのか、中心とするのか定まらないという事である。
数学的に物質の中心は左右の端の1/2と定義するも、現実には物質を構成する原子の個数が奇数なら割り切れない。
こうした事情から、現実的には確率の概念、統計分析は不可避と言える。
アインシュタインは “神はサイコロを振らない” と言って、量子力学が確率の概念を導入する事に終生反対した。
一般相対性理論では、“質量が存在すれば空間が歪む" と表現しているところから完全剛体とは見なしていない。
“空間が歪む" とは前述の机上実験のFig.3_1で示した、重力によってバネが伸びた状態である。
空間の解釈については研究ノート 重力発現モデルを参照されたい。
このように考えると、量子力学に柔性、力エネルギの概念を導入する事が次のステップへ進むキーと考えられる。
|
●量子力学と物理機能モデルの対比
|
粒子と波動の二重性を説明する際に、量子力学と物理機能モデルを対比させると以下のような違いがある。
・量子力学:数学ベース。
・物理機能モデル:物理、力学ベース。
また、物質の最小単位を以下の様にモデル化している。
・量子力学:弦(ひも)
・物理機能モデル:伸縮するバネ(非線形系)
また、波動の捉え方は以下の違いがある。
・量子力学:定在波(横波)
・物理機能モデル:疎密波(縦波)
更に、現象の捉え方は以下の違いがある。
・量子力学:ランダム=確率を導入(非決定論的)
・物理機能モデル:非ランダム=確率は導入しない(決定論的)
本報はド・ブロイの物質波を題材に、量子力学ではなく、物理、力学の視点から解釈を試みたものと言える。
|
もくじへ戻る
 まとめ
まとめ
| ・ |
物理機能モデル手法を用いて物質をモデル化する事により以下の知見が得られた。 |
| ・ |
物質は質量と柔性を持ったバネと見なす事が出来る。 |
| ・ |
バネ単体は線形系であり、振幅の波形は正弦波である。 |
| ・ |
バネ単体で振幅を観測できるのは一端が固定の場合のみである。 |
| ・ |
一端固定とはバネの相手を完全剛体と見なす事に他ならない。 |
| ・ |
現実界に完全剛体は存在せず、物質は2連以上のバネと見なさなければならない。 |
| ・ |
2連以上のバネは非線形系となり、正弦波では無くなる。 |
| ・ |
以上からド・ブロイの物質波は力学的に正弦波では無いという解釈に至った。 |
|
| ・ |
電子の加速、衝突実験で発現する素粒子の質量に巾がある理由を次のように力学的に解釈した。 |
| ・ |
物質は伸縮しており、速度印加のタイミングによって物質が蓄えるエネルギは異なる。 |
| ・ |
電子の伸縮は観測不可能ゆえ、速度印加のタイミングはランダムとなる。 |
| ・ |
電子が蓄えるエネルギ、及び衝突時のエネルギは定まらない。 |
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
[2]:様々なカオスとフラクタル 姫路工業大学環境人間学部 二之宮 弘 著 P1
[3]:研究ノート 力学の双対性から見たプランク定数 五十川晋一 著 2025年
[4]:研究ノート 力学の双対性から見たプランクの公式の導出 五十川晋一 著 2025年
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年
・様々なカオスとフラクタル 姫路工業大学環境人間学部 二之宮 弘 著
・研究ノート 力学の双対性から見たプランク定数 五十川晋一 著 2025年
・研究ノート 力学の双対性から見たプランクの公式の導出 五十川晋一 著 2025年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート 電子レンジの物理モデル化
研究ノート パウリの排他原理のモデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 




















