研究ノート
電子の2重スリット実験に関する仮説
2025.5.31
五十川晋一
|
 目的
目的
2021年時点でも2重スリット実験の追試が行われている。
この実験は1805年頃、ヤングの光の干渉実験として行われ、現れた干渉縞から光は波動であるとの解釈が現れた。
20世紀になると量子力学が発展し、物質は粒子と波動の二重性を持つと解釈されるに至った。
その実証実験として電子を使った実験が1961年に行われ、干渉縞から電子も粒子と波動の性質を持つとされた。
その後に行われた追試は縞模様を干渉縞と解釈し、二つの波動の存在を明らかにする事が目的となった。
その方法は様々だが、いずれも二つの波動を分離して観測するには至っていない。
例として、一個の電子が二つの異なった経路を通るような観測装置が考案されている。
そこで得られた結果は、どちらの経路を通過したかが判別できない時のみ干渉縞が現れるものであった。
ここから、電子の進路を観測する行為自体が電子の振る舞いに影響を与えてしまうと言える。
筆者は、電子を使った実験で発現する縞模様は二つの波動の干渉縞ではないという仮説を立てた。
本報では電子の振る舞いをモデル化して机上実験を行う事で縞模様が現れる仕組みを考察する。
実験は物理機能モデル手法により、粒子と波動の性質を併せ持つ物質を2連のバネとしてモデル化する。
物理機能モデル手法の詳細は補足資料に示した。
 もくじ
もくじ
●電子の振る舞いに関する私案
●机上実験
・万有引力、クーロン力が働く電子の物理機能モデル
・パラメータ・試験条件
●結果
・電子解放時刻をサンプリング時間毎にずらした場合
・電子解放時刻をランダムにした場合
・観測値を丸めた場合
●考察
・ランダムと非ランダム
・フラクタルの性質の打ち止め
・スピンと伸縮の違い
・量子もつれ条件
●まとめ
●参考文献
 電子の振る舞いに関する私案
電子の振る舞いに関する私案
電子の振る舞いについては1925年にパウリの排他原理が示されている。
これは電子はお互いに同じ状態をとらないという考え方である。
現実には電子の状態は観察出来ないので二価性、または量子的な状態と呼ばれている。
有力な例としてスピンの向きというモデルが知られており、お互いに反対の向きを取ると説明されている。
以下に筆者の私案を記す。
ド・ブロイの物質波の考え方を適用し、電子を伸縮しながら運動する物質と見なす。
電子の質量については既知だが、その大きさについては不確定性原理に阻まれて特定する事が出来ない。
しかしながら、大きさ=長さの次元を持てばそれが変化=変形する余地が生まれる。
これは電子を完全剛体とは見なさないという事である。
量子力学では電子の運動量と位置を同時に観測する事が出来ない、という事を不確定性原理と呼んでいる。
伸縮しながら運動する物質の位置は物質自身の両端の位置が定まらないので確定出来ない。
これを不確定性と呼ぶ事も出来る。
排他原理には二つの電子はお互いに重ならない=接触しないという考え方がある。
これに類するものとして数学的にはフラクタルの性質が知られている。
フラクタルの性質が現れる例として、毛細血管や植物の枝分かれ、雪の結晶、リアス式海岸等がある。
こうした性質は細胞分裂や結晶の成長の過程で、隣り合う最末端部は接触しないというルールが必要と考えた。
この結果として、部分と全体の形状が相似形になる事が知られている。 補足資料5参照
筆者はこのルールが発揮される為には、最末端にある原子に付帯する電子にはお互いに接近を感知する仕組みがあると考えた。
お互いに+ーの電荷を持つ電子間にはクーロン力が働いて接近するが、ある至近距離以下では斥力に転じると言われている。[1]
この考え方に基づき、電子の2重スリット実験で発現する縞模様について以下の仮説を立てた。Fig1.の上段参照
・1個の電子を発射し、進路の途中にスリットを置けば発射された電子はそこに付帯する電子を避けようとする。
・2本のスリット様である必要はなく、進路上に障害物を置いたと考える。
・発射された電子の進路は接触を避けてオフセットし、乾板に到達する。
・発射される電子は伸縮しており、伸び縮みのどのタイミングで発射するかは管理出来ない。
・従ってこの実験はランダムとなり、発射される度に電子の進路のオフセット量は異なる。
・このオフセット量がランダムに乾板に記録される。
・規則性を持った等間隔の縞模様が現れる仕組みは別途考察する。
|
この仕組みを実現する為に上記をモデル化し、机上実験を行う。 Fig1.の中、下段参照
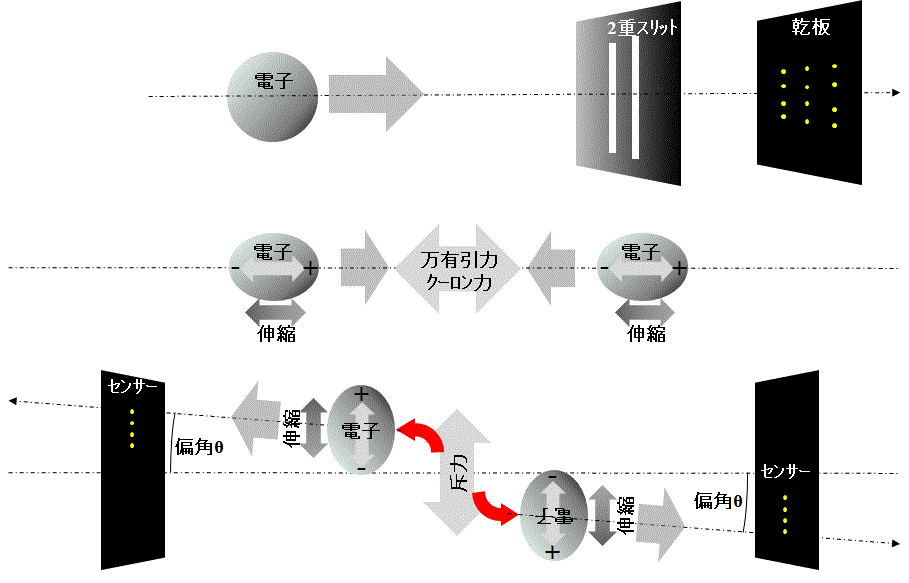
Fig.1
|
・無重力状態で二つの電子を同軸上に置く。
・最初は電子(バネ)の片端を固定し、万有引力、クーロン力を印加すると伸縮を始める。
・この状態でド・ブロイの物質波が模擬される。
・両電子を解放すると伸縮しながら接近する。
・パウリの排他原理を、お互いによけると解釈し、既定の隣接距離になったら斥力を発現させる。
・斥力を進路方向に90度偏向させる事により進路がオフセットされ、お互いの電子は接触を回避する。
・両電子の進路上に二重スリット実験の乾板に相当するセンサー(観測点)を設ける。
・初期進路から偏角θに因るオフセット量を観測する。
|
なお、このモデルは1次元方向に伸縮するバネだが、物理機能モデル手法を用いる事により以下の性質を持つ。
・1個のバネは質量と剛性(バネ定数)を持つ線形系であり、振動は正弦波となる。
・一端を固定した場合は伸縮するだけなので1個のバネで対応できる。
・一端を解放すると伸縮しながら運動する物質となり、これを表現するには基本モデルを直列に2個以上連結する必要がある。
・線形系である1個のバネを連結すると非線形系となり、全長は正弦波ではなく時々刻々複雑な波形を呈する。Fig.2参照
・非線形系に現れる性質として、二重振り子のオモリが描く複雑な軌跡=カオス軌道が知られている。補足資料4参照
・このカオス軌道はフラクタルの性質と同じである。[2]
|
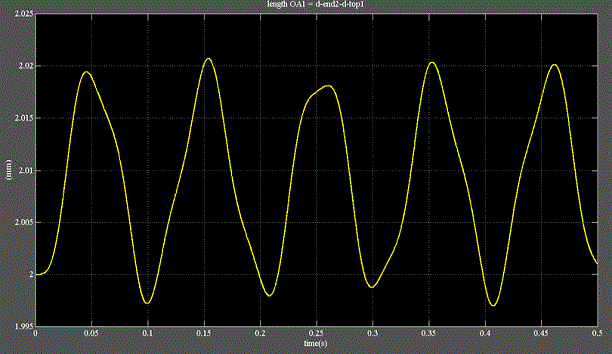
Fig.2
|
もくじへ戻る
 机上実験
机上実験
●万有引力、クーロン力が働く電子の物理機能モデル
モデル図をFig.3に示す。 電子を2連のバネとして表し、2個の電子を同軸上に配してある。
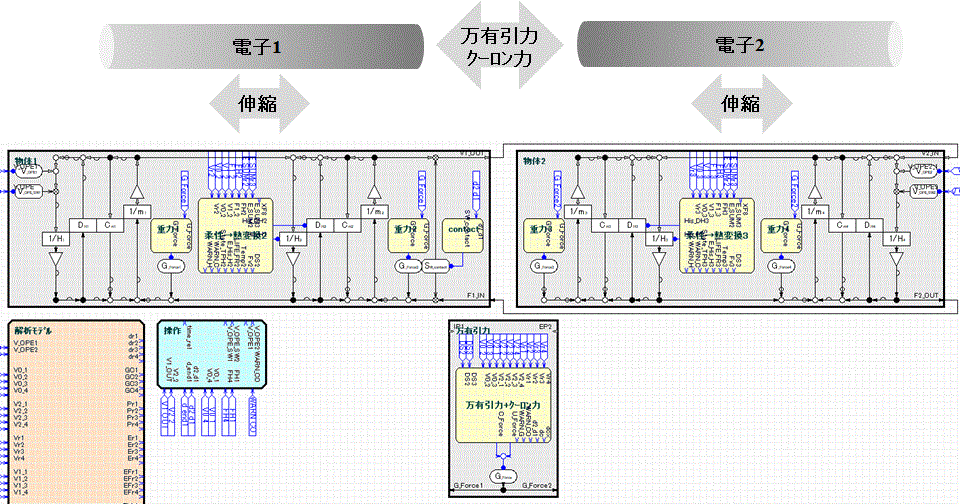
Fig.3
|
●パラメータ・試験条件
●パラメータ:
・電子の質量:9.109e-31 (Kg)、及び電荷:1.602e-19 (As)だが、他の特性値は不明なので仮想の値とする。
・仮想質量m:2.0(kg)
・仮想柔性H:1.0e-4 (mN−1) (剛性kの逆数)
・仮想電荷C:1.602e-7 (As)
・仮想長さL:0.2(m) (万有引力ゼロ時)
・仮想外径Φ:0.2(m)
・万有引力定数:6.672e-11(m3 kg−1 s−2)
・誘電率:8.854e-12 (m3 kg−1 s3 A2)
●試験条件:
・サンプリング時間:1.0e-4 (s)
・2電子の初期隣接距離:2.0(m) Fig.4参照
・片端固定で自由振動させ、解放時刻0.1(s)を起点に、サンプリング時間ずらす操作を200回繰り返す。
・センサー間距離:1.0(m) (2重スリット実験の乾板に相当)
|
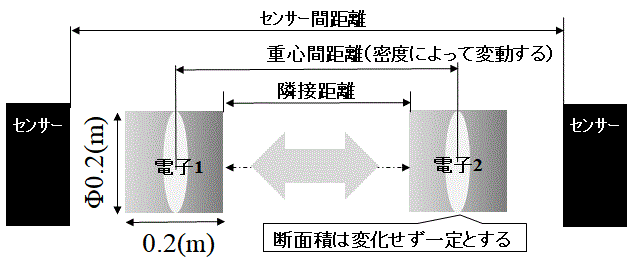
Fig.4
|
もくじへ戻る
 結果
結果
●電子解放時刻をサンプリング時間毎にずらした場合
|
Fig.5参照。
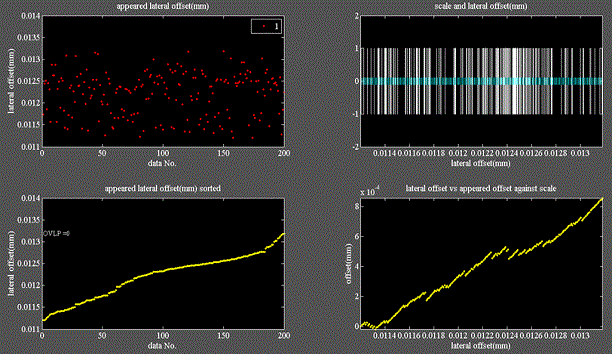
Fig.5
・左上図は200回の試験で得られたオフセット量を試験順にプロットしたものである。
・左下図はそれをソートしたものである。
・右上図はソートしたオフセット量をバーコード様に並べると200個の値は決して重ならない。
・試験を繰り返すとバーコードの隙間は狭くなって行くが、決してゼロにはならない=重ならない。
・これが非線形系に現れるフラクタルの性質である。
・本試験は机上実験であるからバネの伸び、縮みのタイミングに対し、解放時刻を管理している事になる。
・従って結果は再現性があり、確率を論じる必要が無い。
|
|
●電子解放時刻をランダムにした場合
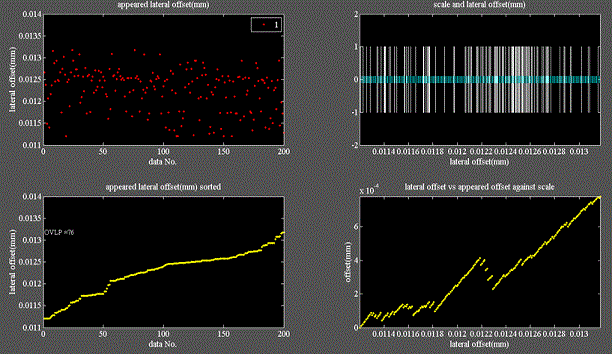
Fig.6
・様式はFig.5と同じである。
・現実の実験では電子の伸び、縮みのタイミングに対し発射のタイミングはランダムになる。
・本実験でこれを模擬すべく乱数を用いて解放時刻をサンプリング゙時間単位にランダムに200回試験を行った結果である。
・バーコード表示は疎になる。
・これは解放時刻が200回中76回同じになったもので、結果的にバーコードの76本が重なったからである。
|
|
●観測値を丸めた場合
|
Fig.7参照。
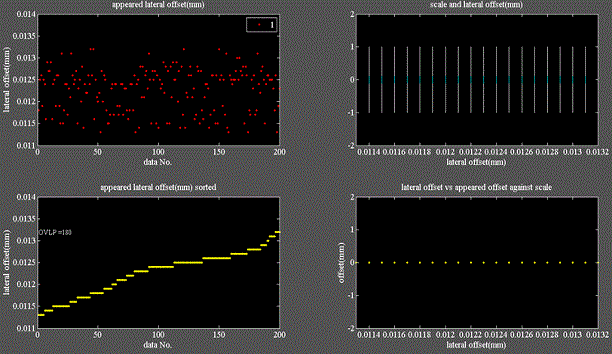
Fig.7
様式はFig.5と同じである。
Fig.5の200個のオフセット量を丸めた結果、180個が同じ値となって重なり、バーコード表示は20本の等間隔となった。
|
|
もくじへ戻る
 考察
考察
●非ランダムとランダム
電子を伸縮しながら運動する物質と見なすと、過去の実験で発現した縞模様は二つの波動の干渉ではないと考えられる。
縞模様は電子の伸縮の伸び、縮みのタイミングと発射のタイミングの組み合わせによって発現すると考えられる。
本報の机上試験を無限に繰り返しても初期進路からのオフセット量は決して同じ値を取らず、重ならない。
従って、縞の間隔は狭まる事はあっても永遠にゼロにはならない。
これはモデルが非線形系であり、フラクタルの性質を持っているからである。
Fig.5で示したオフセット量のバーコードはフラクタルの性質が現れたものと言える。
一方、現実の実験ではオフセット量はランダムとなるので、電子が着地した位置が重なっている例があると推定される。
着地個数が発射回数より少なければ重なっていると判断できる。
これを確認して問題になるのは乾板の解像度(分解能)である。
乾板上では着地した電子によって化学反応が起きるが、解像度は相手の分子がどれだけ密に分布しているかが問題になる。
しかしながら、相手の分子、原子間距離は有限であるから解像度も有限と言える。
一方、フラクタルな性質はどこまで行っても重ならい、すなわち着地点は無限に存在すると言える。
ここから、現実の実験では着地点の間隔が解像度を下回った時点で重なって観測されると考えられる。
これはフラクタルな性質は数学的には無限だが、現実界では物理的に打ち止めになると言える。
この打ち止めとは、実際には着地点は離れていても同一地点と見なす事である。
これは観測値を丸める操作と同じである。
|
●フラクタルの性質の打ち止め
Fig.5で示した200個のオフセット量を丸めた例がFig.7である。
200個のデータの内、180個が同じ値となって重なり、バーコード表示は20本の等間隔となった。
この結果から、過去に行われた実験で発現した縞模様に見られる規則性は乾板の解像度に由来すると考えられる。
これは、電子に限らず万物は非線形系であるが、現実界でフラクタルの性質が打ち止めになった結果と解釈出来る。
人体の毛細血管の総延長は10万Kmを超えると言われているが、目に見えない最末端が存在する。
最末端とはフラクタルの性質の打ち止めと言え、筆者はそれを司っているのが電子の排他原理と解釈した。
以上から、スリットで無くとも電子の進路上に障害物を置くだけで縞模様は発現すると考えられる。
なお、本机上実験の電子モデルは1次元方向に伸縮するモデルだが、現実の電子は3次元方向に伸縮していると考えられる。
|
●スピンと伸縮の違い
従来、量子力学で考えられてきた電子の二価性はスピンの向きというモデルで説明されている。
一方、本報では伸縮の伸びと縮みというモデルである。
物質を伸縮しながら運動するバネと見なすと、蓄えられているエネルギ゙Eは以下のように定義される。
| Ev = 1/2 m・v2 Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.1) |
| Ef = 1/2 H・f2 Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.2) |
| E = Ev + Ef = const. |
(1.3) |
上式は力学の双対性を現し、式(1.3)は対になったエネルギの和は常に一定となる事からエネルギ保存則と呼べる。
補足資料1参照
ここで電子が蓄えているエネルギという観点で見ると、スピンと伸縮では力学的に以下の相違がある。
・スピン:角運動量を想定しているので電子が蓄えているのは、質量に由来する速度(運動)エネルギのみである。
・伸縮:質量に由来する速度エネルギ + 柔性に由来する力エネルギの和である。
このように、スピンのモデルでは柔性に由来する力エネルギは蓄える事が出来ない。
これは電子を完全剛体=柔性=0と見なしているからである。
スピンの向きは量子力学が扱う様々な現象を説明できるが、力学の双対性、エネルギ保存則は成り立っていないと言える。
スピンに替わる考え方については研究ノート パウリの排他原理のモデル化を参照されたい。
|
●量子もつれ条件
本机上実験は二つの電子を全く同じ伸縮のタイミングで解放、接近し、接触を避けて乾板に到達する。
従って、二つの乾板に現れるオフセット量は同一の値、分布になっている。
これは一方の観測結果が得られれば、もう一方は観測しなくとも決まっているという見方が出来る。
これは量子もつれ条件に相当する。
仮に、一方の電子を解放する時刻をズラせば乾板に現れるオフセット量は同一の値、分布にはならない。
現実の2重スリット実験は伸縮のタイミングはランダムになるので、非量子もつれ条件と言える。
|
もくじへ戻る
 まとめ
まとめ
| ・ |
電子が持つ粒子と波動の二重性を物理機能モデル手法により、伸縮しながら運動する2連のバネとしてモデル化した。 |
| ・ |
電子はお互いに重ならないというパウリの排他原理を参考に、二つの電子が接近し、ある隣接距離以下では斥力に転じて接触を回避するモデルを作成した。 |
| ・ |
接触を回避する際に電子の進路がオフセットされる量を観測した。 |
| ・ |
複数回の試験で得られたオフセット量をバーコード様に表すと縞模様が得られた。 |
| ・ |
オフセット量の値を丸めると縞模様は等間隔になった。 |
| ・ |
現実の2重スリット実験で発現する縞模様は二つの波動の干渉では無い。 |
| ・ |
スリットでなくとも電子の進路上に障害物を置くだけで縞模様は発現すると予測される。 |
| ・ |
縞模様が等間隔になる仕組みは乾板の解像度に由来する。 |
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年 P86
[2]:様々なカオスとフラクタル 姫路工業大学環境人間学部 二之宮 弘 著 P1
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年
・様々なカオスとフラクタル 姫路工業大学環境人間学部 二之宮 弘 著
・赤外吸収スペクトルと分子構造研究一バネと玉の振動から形を推測する 岡本裕巳 著 化学と教育 47巻1 号 1999 年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート 電子レンジの物理モデル化
研究ノート パウリの排他原理のモデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 













