Fig.1参照
物質は点ではなく、長さ（空間）を持つ。
密度は均一ではなく、質点（重心）は物質内を移動する。
力fは質点に作用する＝ニュートンの運動の法則
復元力fiは相対速度vrによって生じる＝フックの変形の法則
物質は変形＝伸縮しながら運動する。
柔らかさ＝柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。

Fig.1

●力学の双対性について

物質を伸縮しながら運動するバネと見なすと、バネに蓄えられるエネルギは以下に定義される。 Ev = 1/2 m・v2　　 Ev：速度（運動）エネルギ、m：質量、v：バネ端部速度　　　　　　　　　　　　　　 （1.1） Ef = 1/2 H・f2　　 Ef：力（変形）エネルギ、H：柔性、f：バネ復元力　　　　　　　　　　　　　　　　 （1.2） E = Ev + Ef = const. （1.3） 上式は力学の双対性を現し、式（1.3）は対になったエネルギの和は常に一定となる事からエネルギ保存則と呼べる。 補足資料1参照 ところで、フックの変形の法則は小学校の理科、ニュートンの運動の法則は高校の物理で習う。 両者には以下のような見方がある。 フックの変形の法則　　f = K・L　　f：力（N）、K：剛性（Nm-1）、L：変形量（m）　両辺を時間で微分＊1すると、 df /dt = K・dL/dt　　ここで、dL/dt = vを前に出すと、 v = 1/k・df/dt　　 ここで、1/k = H　に置き換えると、速度vと力fを用いて以下のように表現出来る。 v = H・df/dt　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.4） ニュートンの運動の法則は、 f = m・dv/dt　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.5） 式（1.4）と（1.5）はお互いに速度vと力f、柔性Hと質量mが対称的に入れ替わっている。 ニュートンの運動の法則は質量mに関するもので、これが成り立つ質量とは点であり、長さ、変形という概念と矛盾する。 フックの変形の法則は柔性Hに関するもので、これは静止状態に於けるものであり、運動という概念と矛盾する。 しかしながら、式（1.4）のように速度vを使って表せば運動の概念を含む事になる。 ＊1：補足資料参照 　運動の概念を含むフックの変形の法則の意味合いだが、この法則を実験で導き出す過程を考える。 バネに質量が既知のオモリをぶら下げて伸び量を観測する場合、いきなり静止状態を創出する事は出来ず、手を放せば振動を始めるので振動が収まるまで時間を要する。 あるいは、オモリに手を添えてバネの伸びが止まる位置までゆっくり降ろす操作を考えれば、どんなにゆっくり操作しようと速度を伴う、れっきとした運動である。 つまり、静止状態を創出するにはまず運動ありきという見方である。 　一方、地球上でバネの上端を固定して垂直に吊るせば、無重力空間に置いた長さ（自然長）より伸びる。 ニュートンの運動の法則によれば、重力は質点 = 重心に作用するが、その位置は無重力の場合は数学的に両端から1/2に在るが、地球上で垂直に吊るした場合は1/2では無く、若干下にズレる。 これは重力を受けてバネが伸びる際に密度は均一ではなく、固定端から座標が下るほど大きくなるからである。 鉛直座標から見た物質の密度は非線形であると言える。Fig.2参照 逆に非線形な密度の座標上の観測者から線形の鉛直座標を見れば歪んでいるように見えるかもしれない。 これはアインシュタインが一般相対性理論で行った、時間と空間の座標の入れ替えと同じ意味合いである。 質量が存在すればその周囲の空間は歪む、という見方は、質量を持ったバネを吊るせば伸びる、と同義である。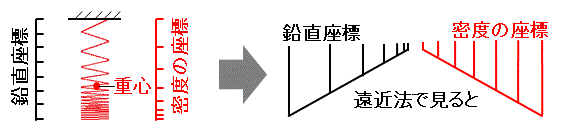 Fig.2 　この事実は冒頭のFig.1で示したように、物質は点ではなく、現実には長さを持ち、どんなに微小であっても変形を伴う事を示している。 変形の概念を含むニュートンの運動の法則の意味合いも、ここに対となって存在すると言う事である。 こうした見方をすると式（1.4）と（1.5）は変形と運動という概念で対等に論じる事が出来、お互いに双対の関係にあると表現出来る。 力学の双対性とは法則ではなく、物事の見方なのである。 　次に、上記の見方に沿って相対性理論を考えてみる。 Ev = m・c2　　c ：限界速度 = 光速(ms-1)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.6） 式（1.6）は特殊相対性理論の式であり、質量mと限界速度cに関するものと見ればこれを、 　・質量m→柔性H 　・限界速度c→限界力fv（物質を繋ぎとめて置こうとする力と仮定する） に入れ換えると、式（1.7）が与えられる。 Ef = H・Fv2　　Fv：限界力(N)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.7） 一般相対性理論に於ける、質量mが存在すれば空間が歪むと言う表現は、変形、すなわち長さという概念から生まれる。 式（1.7）は一般相対性理論を柔性Hと力、すなわちフックの変形の法則で表現したものと言える。 力学に於ける双対性とは、以下が対になるものである。 　・速度v　vs　力f 　・速度エネルギEv　vs　力エネルギEf 　・質量m　vs　柔性H 　・運動　vs　変形 　・運動量　vs　変形量（変位） 　・ニュートンの運動の法則　vs　フックの変形の法則 　・特殊相対性理論　vs　一般相対性理論 そして、アインシュタインの両相対性理論は、以下のような見方が出来る。 　・特殊相対性理論：質点の運動 = 粒子として見た時にニュートンの運動の法則から外れる極限状態 　・一般相対性理論：長さを持った空間の変形 = 波動として見た時にフックの変形の法則から外れる極限状態 　・フックの変形の法則から外れる極限状態とは、物質が変位と力が比例しない塑性変形域に入るという事である。[1] 　・相対的に質量mが優勢になれば粒子のように振る舞い、柔性Hが優勢になれば波動のように振る舞う。[2] 　・空間とは実体の有るものと無いもの、両方の意味合いがある。 更に、力学の双対性には重要なルールが存在する。Fig.3参照 　・物理的に対象（空間）を外部から操作、観測出来るのは速度だけである。 　・力は対象（空間）の内部に生じるもので、外部から操作、観測する事は出来ない。 　・こうした性質を表す、内包量、外延量という概念が存在する。補足資料3参照 Fig.3 　工学の分野では力の代用特性として歪＝変形量＝変位を測っているが、変位とは速度の時間積分量である。 変位が信頼できるのはフックの変形の法則が成り立つ線形範囲＝弾性変形域に限られる。 同時に速度が信頼できるのも弾性変形域に限られると言える。 力学上の弾性変形域とは数学的にxとyが比例する線形性が保証された領域と言える。 そもそも速度とは数学的に距離＝長さを時間で除した量であり、基準となる長さ＝空間が変形すれば信頼出来ない。 競泳プールが柔らかいビニール製なら泳者の波動によって変形してしまい、タイムは信頼出来ないのと同じである。 　・長さとは速度を時間で積分した量である。 　・速度とは長さを時間で微分した量である。 　・時間とは長さを速度で微分した量である。 　これは長さ、速度、時間、そして積分と微分が堂々巡り＝入れ替わると言え、これも双対の関係と言える。 数学に於いて、sinとcosはお互いに積分と微分の関係になっている事も同様である。 sinとcosの波形はπ/2だけ位相がずれているが、力学上の振動現象に於いて速度と力の波形も同様である。 これがアインシュタインが一般相対性理論で行った、時間と空間＝長さの座標の入れ替えのアイデアである。 このような見方をすると両相対性理論は、物質が弾性変形域か？塑性変形域か？という状態を問うていると言える。 これは物質（原子）が崩壊するかしないかという境界と言い換えることが出来る。 物質の最小単位である素粒子から天体、それが無数に点在する宇宙に至るまで、運動と変形、粒子と波動の二重性は切り分ける事が出来ないと言える。

エネルギとプランク定数についての式をあらためて記す、 E = h・ν　　h：プランク定数　 ν：振動数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.8） 式（1.6）と（1.8）は、前者は対象を粒子、後者は波動として捉えていると言われているが、振動数νを前に出すと、 ν = m・c2 /h　　振動数は質量mに比例する。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.9） 式（1.7）と（1.8）から同様に、 ν = H・Fv2/h　　振動数は柔性Hに比例する。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.10） ここで式（1.9）と（1.10）の両辺の積を取ると、 ν2 = m・c2/h・H・Fv2/h 　両辺の平方根を取り、 ν = √(mH)・c・Fv/h　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.11） 一方、一般力学に於けるいわゆるバネ・マス系の自由振動に於ける振動数fは以下の関係にある。 f = 1/(2π・√(mH))　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.12） ここで量子力学に於ける振動数ν（1.11）と一般力学に於ける振動数f（1.12）は以下のように矛盾している。 　・量子力学　振動数ν：質量mと柔性Hの積に比例する。 　・一般力学　振動数f：質量mと柔性Hの積に反比例する。 ニュートンの運動の法則　vs　フックの変形の法則はお互いに矛盾を抱えているが双対関係にある事に倣えば、量子力学と一般力学もお互いに双対の関係にあると言う見方が出来る。 そこで、式（1.11）と（1.12）を等しいと置き、 √(mH)・c・Fv/h = 1/2π・1/√(mH)　 両辺に√(mH)を掛けて、 m・H = 1/2・π・h/c・Fv 　プランク定数hを前に出すと、 h = 2π・c・Fv・m・H = const.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.13） π、cは定数であるから以下の関係が得られる。 Fv・H・m = const.　　注：柔性Hの位置を変えてある　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.14） Fv・Hなる値は実測されておらず、未知の値であるが、Fv・H = Fv/k　である。 この意味合いは、本報ではFvは物質を繋ぎとめて置こうとする限界力（材料力学で弾性変形域から塑性変形域に遷移する降伏点に相当）と考えているので、これを剛性Kで除せばフックの変形の法則が成り立つ限界長さL = 限界変形量と言える。 このように考えると式（1.14）は以下のように書き直せる。 L・m = const.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.15） これは質量mを原子量と置けば、原子が崩壊する際の限界変形量と原子量の積は一定であると解釈出来る。 すなわち、Fv・H = Lなる値は未知だが、原子量が大きい元素ほど崩壊に至る際の限界変形量は小さい＝柔性Hも小さい＝剛性Kは大きい＝硬いと言う見方が出来る。 あらためてプランク定数hを表す式（1.13）は以下のように表現出来る。 h = 2π・c・L・m = const.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.16） さらに式（1.16）のmの位置をcの隣に移動すると。 h = 2π・c・m・L = const.　　c・m：限界運動量、L:限界変形量 = 変位　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 この式の意味する所は、原子の限界運動量と限界変形量の積は一定である。 言い換えると、原子崩壊に於ける運動量と変形量の積は一定である。 量子力学では運動量と変位は同時に確定出来ないと言う不確定性原理があるが、原子崩壊と言う限界条件では、 L = h/(2π・c・m) 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.17） となり、限界変形量（変位）が定義出来る。　例として水素原子1個の質量からLを求めると、　 　h = 6.62607015×10-34 　光速c = 299792458（m/s）　　ここでの光速とは質点の移動速度ではなく、疎密波の伝搬速度の限界値と言える。 　水素原子量 = 1.00784（g） 　1モル = 6.02×1023　　 　L = (6.62607015 ×10−34 ×6.02 ×1023 )/(2π ×299792458 ×1.00784 ) = 2.10×10-19（m） なお、限界変形量は原子量に反比例するが、これと同じ性質を示す物性値としては比熱（J/Kg/k）があり、物質が蓄える熱エネルギEtは以下の式で表される。Fig.4、5参照 Et = m・Cp・T　　Cp:比熱(JKg-1k-1)、T：温度(k)　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （1.18） ここで　m・Cp = const. になるから熱エネルギEtは温度Tに比例する。 これはプランクが研究していた溶鉱炉内の物質が輻射するエネルギは元素＝材質には依存せず、温度Tだけで決まる事と符合する。 Fig.4 　Fig.5

・	プランク定数は力学の双対性から、以下の表し方が出来る。 　E：エネルギ 　h：プランク定数 　ν：振動数 　m：質量 　H：柔性=1／K　K：剛性 　c：限界速度=光速 　Fv：限界力（物質を繋ぎとめて置こうとする力） 　L：限界変形量（原子が塑性変形＝崩壊に至る直前の変形量）　と置くと、 　h = m・c2/ν 　h = H・Fv2/ν 　h = 2π・c・Fv・H・m 　h = 2π・c・L・m
・	最後の式からプランク定数hは原子の限界変形量Lと質量mの積で表され、一定である事を示している。
・	この式から以下の仮説を立てた。
・	限界変形量L、柔性Hは原子量に反比例する＝重い元素ほど剛性が大きい＝硬い。