研究ノート
物質の柔性が粒子と波動性に及ぼす影響
2025.9.30
五十川晋一
|
 目的
目的
力学における双対性(対称性)として質量mと柔性Hという二つの特性値がある。
柔性H=1/剛性kであり、一般力学では質量mと剛性kは振動現象を扱う際に必須であり、自由振動の場合、
固有周期 = 2π√(mH) または 2π √(m/k)の関係にある。
教科書のバネ・マスの自由振動の解説では下図Aのように質量mはオモリ、剛性kはバネと切り分けている。
これはオモリの質量mに対して相対的にバネの剛性kが小さい=柔らかいバネをイメージするかもしれない。
しかしながら現実はバネ自身にも質量mがある事を考えれば、下図Bのように表す事も出来る。
Bの場合、このバネは柔らかいのだろうか? 殆ど伸縮しない硬いバネかもしれない。
現実の機械はオモリがぶら下がる構造とは限らず、Bのようにバネ単体で物理現象を表現出来なければならない。
力学における双対性に基づいた物理機能モデルでは、機械を構成する全ての要素についてBのように表す。
これは物質をバネと見なすという事であり、例えばボルトによる締結はバネでバネを挟み付ける事に他ならない。
またそうすることで電気・電磁気学とのシームレスなモデリングが可能である。
一方、量子力学では光電効果を素粒子の粒子と波動の二重性として説明している。
ド・ブロイは1924年に物質波という概念を提示し、粒子と波動の二重性を素粒子のみならず一般の物質まで広げた。
物質波は、“どんな物質も振動を伴っている” と解釈するものだが、素粒子以外の一般の物質でそれを実験的に検証することは難しい。
また柔らかい=柔性Hが大きい物質は捉えどころが無く、機械としては適切に機能を果たす事が難しい。
例外としては米国で1945年に玩具として登場したSLINKYがあり、非常に柔らかい=柔性Hが大きいバネである。
これを教材とし、物理機能モデルにより柔らかいバネの挙動を模擬することで物質波の理解を試みる。
なお、物理機能モデル手法の詳細は補足資料に示した。
本報は2024年7月30に開催された、機械学会交通物流部門 連続講習会No.24-53 で筆者が発表した資料 "物体の柔性が粒子と波動性に及ぼす影響" に修正、加筆したものである。
 もくじ
もくじ
●柔らかい物質について
●机上実験
・柔らかい物質の物理機能モデル
・パラメータ
・試験条件
・結果
●考察
・柔性Hが大きいほど、速度、変位の波形に振動が乗る
・運動と変形が同時に起きている時のエネルギについて
・現場での困り事
・柔性Hが大きいほど落下は遅くなる
・量子力学に於ける課題
●まとめ
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[1]
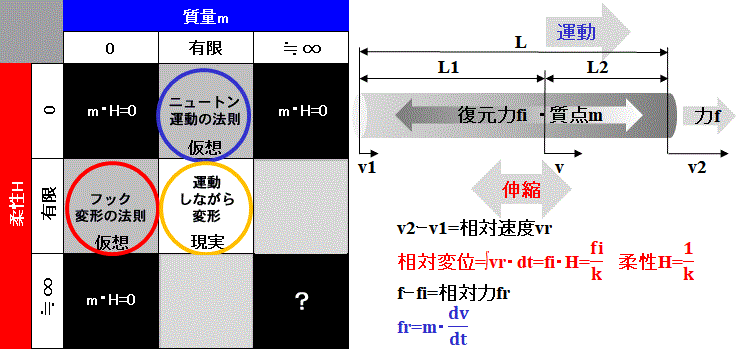
Fig.1
|
もくじへ戻る
 机上実験
机上実験
●柔らかい物質の物理機能モデル
Fig.2にモデル図を示す。
柔らかい物質を垂直に吊るすと重力が作用して伸びる。
上端ほど伸びが大きい(密度が低い)様相を模擬するために、同一諸元のバネを2連にしてある。
こうする事で上側、下側のバネが其々、伸び(変位)が異なる事が表現される。
勿論、連結数を増やせばより正確な挙動を観察する事が出来る。
注:実験では減衰しないように粘性抵抗係数Cm、塑性抵抗係数DH(これらエネルギ消費要素)はゼロとしてある。
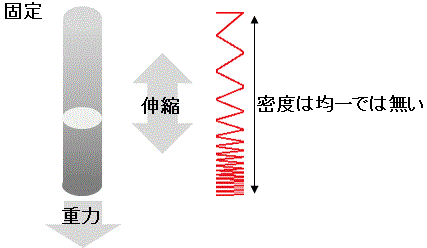
 Fig.2
Fig.2
|
|
●パラメータ
・質量m:1.0(kg)
・柔性H:1.0e−5、1.0e−3、1.0e−2(mN−1)の3水準
・長さL:0.1 (m) (万有引力ゼロ時)
・外径Φ:0.04(m)
・固定端高さ:20(m)(地上までの距離)
・温度:0°(k)絶対零度
| 柔性(mN−1) | 固有振動数(s−1) | 長さ(m)垂直吊るし時 | 伸び率(%) |
| 1.0e−5 | 70.423 | 0.1003 | 0.297 |
| 1.0e−3 | 7.097 | 0.1297 | 29.677 |
| 1.0e−2 | 2.244 | 0.3968 | 296.777 |
|
●試験条件
・伸び切った状態から解放して自由落下させる。
・サンプリング時間:0.1msec
|
●結果
Fig.3-1~3-3に自由落下時の物体の各物理量の時系列波形を示す。
横軸は全て時間とし、落下開始から1秒間を表示している。
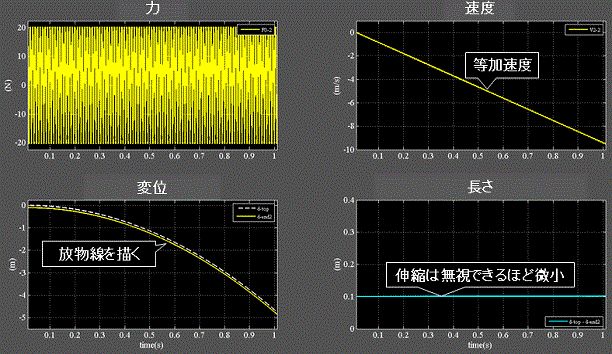
Fig.3-1 柔性H:1.0e−5(mN−1)
・左上:力(復元力)は周期的に変動する。
・右上:速度(下向きが負)はニュートンの運動の法則に従い、等加速度で増加。
・右下:物体の長さの変化=伸縮は無視できるほど微小。
・左下:変位はニュートンの運動の法則に倣い放物線を描く。(破線:バネの上端、実線:下端)
・物体は粒子の性質を示す。
|
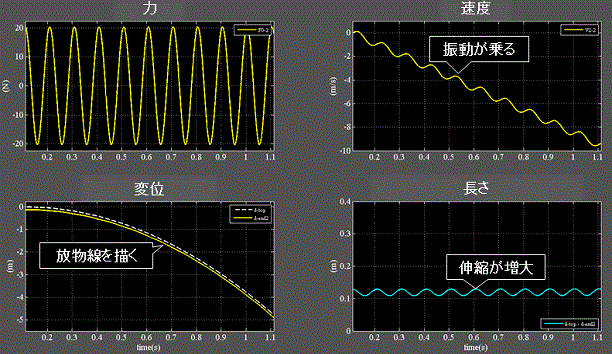
Fig.3-2 柔性H:1.0e−3(mN−1)
・左上:力(復元力)の周期はFig.3-1より長くなる。
・右上:速度(下向きが負)は等加速度で増加するが、振動が乗る。
・右下:物体の長さの変化=伸縮が増大。(右下)
・左下:変位はニュートンの運動の法則に倣い放物線を描くが、僅かに歪みが生じる。
・物体は粒子と波動の中間的な性質を示す。
|
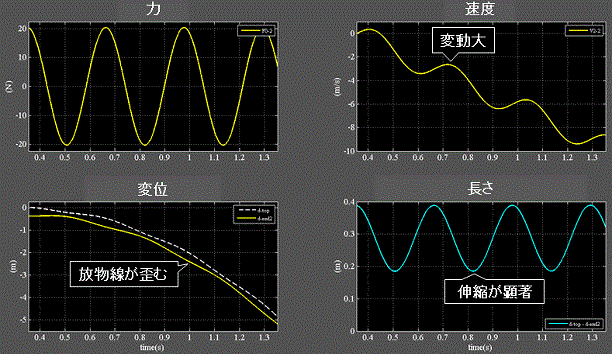
Fig.3-3 柔性H:1.0e−2(mN−1)
・左上:力(復元力)の周期はFig.3-1より更に長くなる。
・右上:速度(下向きが負)は増加するが変動が大きい。
・右下:伸縮が顕著。
・左下:変位は上端(破線)と下端(実線)は同期せず、放物線が歪む=ニュートンの運動の法則に従わない。
・物体は波動の性質を示す。
|
物質全般は絶対零度以上の温度にあるとき、熱エネルギを蓄え、かつ伸縮している。*1
まず、伸縮している物質の力学的エネルギEは以下のように定義される。
| Ev = 1/2 m・v2 |
Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.1) |
| Ef = 1/2 H・f2 |
Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.2) |
| E = Ev + Ef = const. |
|
(1.3) |
上式は力学の双対性を現し、式(1.3)は対になったエネルギの和は常に一定となる事からエネルギ保存則と呼べる。
補足資料1参照
なお、本実験では自由落下の挙動のみを観察したいので熱エネルギはゼロ=絶対零度の条件としており、純粋に重力によって物質の伸縮と落下が同時に起きている。
*1:ド・ブロイの物質波と言え、物質全般はバネと見なす事が出来る。
次にFig.4-1~4-3に物体が蓄えている力エネルギ、速度エネルギの時系列波形を示す。
横軸は全て時間としてあるが、解放して自由落下が始まる時刻から表示してある。
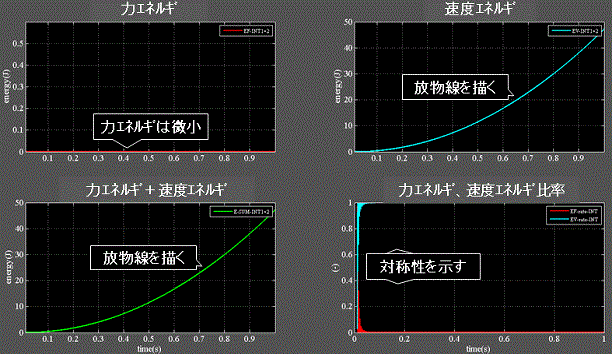
Fig.4-1 柔性H:1.0e−5(mN−1)
・左上:力エネルギは微小である。
・右上:速度エネルギは速度vの2乗に比例するので放物線を描く。
・左下:力エネルギ+速度エネルギも放物線を描く。
・右下:力エネルギ+速度エネルギを1とした時の両エネルギの比率は対称性を示す=一方が増えれば他方は減る。
|
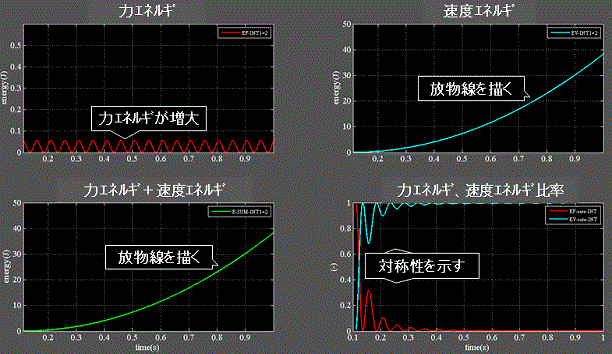
Fig.4-2 柔性H:1.0e−3(mN−1)
・左上:力エネルギが増大。
・右上:速度エネルギは速度vの2乗に比例するので放物線を描く。
・左下:力エネルギ+速度エネルギも放物線を描く。
・右下:力エネルギ+速度エネルギを1とした時の両エネルギの比率の振動周期はFig.4-1より長くなる。
|
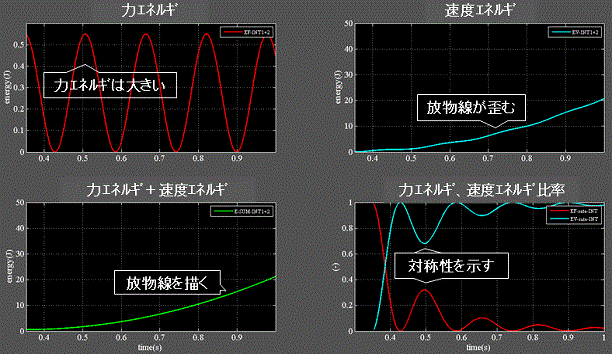
Fig.4-3 柔性H:1.0e−2(mN−1)
・左上:力エネルギは更に増大。
・右上:速度エネルギの放物線が歪む
・左下:力エネルギ+速度エネルギは放物線を描く
・右下:力エネルギ+速度エネルギを1とした時の両エネルギの比率の振動周期はFig.4-1より更に長くなる。
|
実験結果をまとめると、柔性Hを1.0e−5→1.0e−3→1.0e−2(mN−1)と大きく(柔らかく)するほど、
・速度エネルギに対して力エネルギが相対的に優勢になる。
・速度エネルギ波形に振動(ゆらぎ)が乗る。
・時間とバネの長さ=空間が相互に伸縮している事が明瞭になる。(ズームされる)
・時間軸に対して速度エネルギと力エネルギの対称性が明瞭になる。(ズームされる)
・物質が蓄えているエネルギの観測はリアル実験では不可能だが、机上実験ゆえに可能である。
|
もくじへ戻る
 考察
考察
●柔性Hが大きいほど、速度、変位の波形に振動が乗る
物体の自由落下時の時間に対する変位はニュートンの運動の法則に従えば放物線を描く筈だが、物理機能モデルでは柔性H、すなわちフックの変形の法則を対にしているので、柔性Hを大きくすれば振動が乗り、その影響が現れる。
質量mに対して柔性Hが相対的に大きくなると物体は粒子よりも波動の性質が増すと解釈できる。
これはド・ブロイの物質波と同じ意味合いと考えられる。
すなわち、質量mと柔性Hが対を成すことで、物質は本来振動(伸縮)を伴うと言える。
これは運動と変形は同時に起きている=両者は対になっており、本来、切り分けられないと解釈できる。
力学における双対性(対称性)を踏まえると、質量mと柔性Hの比率に応じて粒子の性質が顕著になったり、波動の性質が顕著になったりすると言える。
これは電磁気学において、電場と磁場が対になっており、電気回路に蓄えられる静電エネルギと電磁エネルギはコンデンサの静電容量C(キャパシタンス)とコイルのL(インダクタンス)の比率に左右される事に相当する。
量子力学では光電効果を素粒子の粒子と波動の二重性として説明しているが、力学全般に通じると言って良い。
|
●運動と変形が同時に起きている時のエネルギについて
Fig.4-1で示したように、速度エネルギは速度vの2乗に比例するので放物線を描く事になる。
次に柔性Hが大きく、柔らかくなるとFig.4-2~4-3で示したように力エネルギが優勢になり、速度エネルギに歪みが現れる。
これはエネルギ保存則=力エネルギ+速度エネルギ=const.に基づき、相対的に力エネルギの寄与度が増したと解釈できる。
なお、左下図の力エネルギ+速度エネルギは一定ではなく、放物線が現れるのは以下の理由である。
・式(1.3)は物体がその場に静止していようが運動していようが、伸縮(変形)する物体に於いて常に成り立つ。
・この関係に、落下(運動)現象は物体の質量mと地球の質量との間に作用する重力加速度が重ね合される。
|
●現場での困り事
現場での困り事は設計目標を達成した筈の商品が市場に出てから問題を起こす事である。
その原因の本質は機械が持っているエネルギ(瞬時) *2の変換効率~伝達効率が低過ぎたか、市場で要求されるエネルギを見誤った場合である。
自動車を例にとれば、前者は燃費の悪さ、後者は動力性能の悪さ、寿命の短さとして指摘を受ける。
不幸にも商品の寿命が短かった場合、その原因は疲労強度にあり、これはフックの変形の法則の線形範囲を超えて塑性域に入っている事の証左である。
疲労破壊とは変形の繰り返しであり、ここからも運動と変形が同時に起きていると考える意味合いが見えてくる。
従って、少なくとも疲労限度内にあることを確認するにはフックの変形の法則=柔性Hを省略することは出来ないと言える。 *3
このように考えるなら、少なくとも設計に用いる際のモデリングでは柔性Hを省略すべきでは無い。
物理機能モデルは、機構、流体、熱力学、電磁気学だけでなく、寿命計算のような材料力学的な視点も踏まえた設計に威力を発揮する手法と言える。
*2:エネルギ(瞬時)とは単位時間当たり(J/s)という意味でパワJ/s)と同義
*3:元祖SLINKYは金属製だが、遊んでいるうちに永久変形=歪が残って元の縮んだ状態に戻らなくなったり、縁日で売られているプラスティック製は折れてしまう事がある。
|
●柔性Hが大きいほど落下は遅くなる
Fig.3-1~3-3の左下図の変位を比較すると、上端を解放してから下端が落下し始めるのが遅れる事が判る。
Fig.3-3の左下図をズームしたFig.5-1、及びアニメーションFig.5-2参照
ニュートンの運動の法則に従えば、時間に対する物体の落下位置は一定の筈である。
ニュートンは物体を長さを持たない質点として扱っているからである。
冒頭のFig.1で述べたように現実には物体には長さがあるのでバネの上端と下端では挙動が異なるという事である。
これはバネが伸び切った状態は力エネルギが最大、速度エネルギ=0の状態であるが、その時刻で上端を解放するとバネは縮み過程に入り、力エネルギは速度エネルギへ変換が始まり上端の速度が増加し始める。
一方、下端は残っている力エネルギ=復元力によって直ぐには落下しない状況となる。
物体の伸縮とは、エネルギ保存則=力エネルギ+速度エネルギ=const.に従って自身に蓄えられている力エネルギと速度エネルギの交換が行われている=一方が増えれば他方は減るという現象と言える。
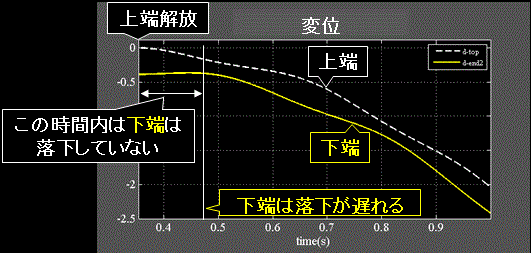
Fig.5-1
|

Fig.5-2
アインシュタインの一般相対性理論によれば、物体と地球の間に働く重力加速度は両者の距離=高度に依存するので厳密には一定では無く、スカイツリーの最上階では時間の進み方が地上より速い事が実験で検証されている。
本報の物理機能モデルによる試験は柔性H、つまりフックの変形の法則を考慮する事で時間の進み方が異なる事を示したものと言える。
|
●量子力学に於ける課題
量子力学の課題に、量子を点ではなくひもに喩えたひも理論、超弦理論があるが、これらは実験的検証が困難という事情がある。
リアル実験を想定しても非常に大きなエネルギが必要になり、現実的には限界がある。
本報の課題は機械工学の分野で生まれた物理機能モデル手法を用いて物質の挙動をエネルギの視点で解釈するものである。
前述のように物質が蓄えているエネルギを観測する術は無く、机上実験なら可能である。
物理機能モデルでは物質が蓄えているエネルギを、速度(運動)エネルギと力(変形)エネルギに分離して計算する事が出来る。
一方、現状の量子力学では質量が蓄える運動エネルギは考慮しているが、柔性が蓄える力(変形)エネルギが考慮されていない。
これは不確定性原理に阻まれて、量子の変形量を観測できないという事情もあると考えられる。
これは機械工学の分野で見ると、伸縮しているバネの両端の位置は任意に定まらないという事と同義である。
しかしながら、現実に設計される機械に限らず、宇宙空間に存在するあらゆる物体が伸縮していると言っても、微弱な為に実害が無いと言える。
但し、物質の伸縮は微弱と言えどもミクロな視点では物質の内部では疲労破壊が進行しており、機械の寿命予測が万全であるとは言えないのである。
これは、実害無いとは言い切れない分野が存在するという事である。
例えば、航空機は使い方が管理されているので、疲労寿命も管理下にあり、寿命が来る前に部品を交換する事で安全が保たれている。
一方、自動車の使われ方は個人に因って千差万別であり、疲労寿命の管理の困難さゆえに起きて欲しくない故障は設計者の裁量に任されていると言える。
このように考えると、量子力学上の課題は力(変形)エネルギを組み込む事でブレークスルー可能ではないだろうか?
なお、疲労破壊については既研究ノート 物質破壊(崩壊)のモデル化を参照されたい。
|
もくじへ戻る
 まとめ
まとめ
| ・ |
物理機能モデルで柔らかい物体の伸びきり→自由落下を模擬することで以下の知見を得た。
|
| ・ |
柔性の増大と供に
・時間と速度の関係は等加速度ではなく、振動が乗る。
・時間と変位の関係は歪んだ放物線を描く。
・速度エネルギ波形に振動が乗る。
・速度エネルギに対して相対的に力エネルギの影響が大きくなる。
・粒子としての性質から波動としての性質が大きくなる。
・落下は遅くなる。
|
| ・ |
ド・ブロイの物質波という概念に示される粒子と波動の二重性が確認できた。
|
| ・ |
粒子と波動の二重性は ”運動と変形は同時に起きている” と同義である。
|
| ・ |
アインシュタインの一般相対性理論による時間と空間の伸縮が確認できた。
|
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:機械学会交通物流部門 連続講習会No.24-53 資料
"物体の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域模擬のための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・研究ノート 物質破壊(崩壊)のモデル化 五十川晋一 著 2025年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年
・赤外吸収スペクトルと分子構造研究一バネと玉の振動から形を推測する 岡本裕巳 著 化学と教育 47巻1 号 1999 年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート 電子レンジの物理モデル化
研究ノート パウリの排他原理のモデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 

















