光格子時計に用いる原子の要件
ネット上で「なぜ光格子時計ではストロンチウム原子が使われるのか?」という疑問を目にしたのですが,これを一般向けに解説したものはあまり見当たらないので,自分なりに説明してみようと思います.時計遷移
光周波数帯の原子時計では,周波数基準として選ばれた基底状態 → 励起状態の遷移(時計遷移)の確率が最大になるように時計レーザの周波数を制御します. プランク定数を h (6.62607015×10-34J・s)とすると,時計遷移周波数は以下の式で与えられます.νc = (We - Wg)/hここで,Wg は基底状態,We は励起状態のエネルギー準位です.
時計遷移の線幅を Δν とする時,
Q = νc/Δνが大きい程,周波数安定度は良くなります.
線幅が広くなる原因は様々ですが,原子の熱運動によるドップラー広がりなどを取り除くと,励起状態の原子が光を自然放出して基底状態に遷移する寿命の逆数(自然幅)および原子とレーザ光の相互作用時間の逆数(相互作用時間幅)で決まります. 従って,高い周波数安定度を得るためには,(相互作用時間幅に比べて)自然幅が十分狭い励起状態への遷移を使う事が必要です.
[要件1]時計遷移では自然幅が非常に狭い(寿命が非常に長い)励起状態が必要
光格子と魔法波長
レーザ光(波長 λL)の電界強度を EL とすると,その中にある基底状態の原子は分極して,電気双極子 pg(λL) = αg(λL)EL が誘起されます. ここで,αg は基底状態の分極率です. この電気双極子と電界の相互作用により,基底状態のエネルギー準位 Wg は,W'g = Wg - αg(λL)|EL|2/2と変化します. これは「シュタルクシフト」と呼ばれます.
電界強度が空間的に均一でない場合,原子はエネルギー準位が低くなる方向(αg(λL) > 0 ならば,光の強度 |E(λL)|2 が大きくなる方向)に双極子力を受けます. レーザ光を干渉させて定在波を作ると,定在波の腹の個所でエネルギー準位が極小になるので,そこに原子がトラップされます. 定在波の腹にトラップされた原子は格子状に並ぶので「光格子」と呼ばれます.
光格子にトラップされた原子の励起状態のエネルギー準位 We は基底状態と同様にシュタルクシフトします.
W'e = We - αe(λL)|EL|2/2ここで,αe は励起状態の分極率です. その結果,光格子中の原子の時計遷移周波数は
ν'c = νc - {αe(λL) - αg(λL)}|EL|2/(2h)と変化してしまうので,このままでは正確な時計遷移周波数は得られません. ただし,分極率は波長 λL に依存するので,励起状態と基底状態のシュタルクシフトがキャンセルされる「魔法波長」に設定できれば,高い周波数確度が得られます.
[要件2]時計遷移に用いる励起状態と基底状態に対して魔法波長が存在する事が必要
レーザ冷却
光格子に原子をトラップする前段階として,高温(速度が数百m/s)の原子をµKオーダまでレーザ冷却する必要があります(原子の温度が高いと光格子にトラップできません).レーザ冷却では,最初にゼーマン減速を用いて原子ビームを冷却します. 原子ビームがある程度冷却されたら,次に磁気光学トラップ(MOT: Magneto-Optical Trap)を用いて更に冷却しながら原子を一箇所にトラップします.
原子の進行方向から逆向きにレーザ光(原子の共鳴周波数より少し低く設定)を照射すると,原子はレーザ光を吸収して基底状態から励起状態に遷移し,吸収した光子の分だけ運動量が減少します. その後,励起状態の原子は光を自然放出して基底状態に戻り,再びレーザ光を吸収します. レーザ光の吸収と自然放出を何度も繰り返す事により原子の運動量が減少するので,寿命が短い励起状態への遷移を使えば,短時間で原子を冷却する事ができます.
一方,MOTを用いて原子を冷却できる限界(ドップラー冷却限界)は
TD = hΔνn/(2kB)で与えられます. ここで,Δνn は自然幅,kB はボルツマン定数(1.380649×10-23J/K)です.
この式を使って計算してみると,
Δνn = 1MHz ならば,TD = 24µKとなるので,自然幅が狭い励起状態への遷移を使った方が原子をより冷却する事ができます.
Δνn = 100kHz ならば,TD = 2.4µK
Δνn = 10kHz ならば,TD = 240nK
そこで,光格子時計では2段階のレーザ冷却を組み合わせています. 1次レーザ冷却(ゼーマン減速およびMOT)では自然幅が広い励起状態への遷移を使って急速に冷却し,2次レーザ冷却(MOT)では自然幅が少し狭い励起状態への遷移を使って徐々にµKオーダまで冷却します.
[要件3]1次レーザ冷却では自然幅が広い(寿命が短い)励起状態が必要
[要件4]2次レーザ冷却では自然幅が少し狭い(寿命が少し長い)励起状態が必要
ストロンチウム原子
ストロンチウム(Sr)には4種類の安定同位体が有りますが,現在の光格子時計で主に用いられているのは原子核が38個の陽子と49個の中性子(合計87個の核子)から成る87Srです.陽子の数が偶数で中性子の数が奇数ならば,原子核のスピンは必ず半整数(奇数×1/2)になります. 87Srの場合,原子核はスピン I(I = 9/2)を有します.
これ以外の安定同位体(84Sr,86Sr,88Sr)の原子核は陽子の数と中性子の数が両方とも偶数なので,核スピンは 0 になります.
Sr原子は38個の電子を持っており,その内の36個は1s軌道から4p軌道までを占めています.
残りの2個の電子(価電子)は通常は5s軌道にあります. これは価電子のエネルギー準位が最も低い基底状態です. これに対し,5p軌道より上は外部から何らかの形(たとえば光)でエネルギーを与えられた励起状態です.
基底状態では2個の価電子は共に5s軌道にあり,「パウリの排他律」によりスピンは必ず逆向きなので,2個の価電子の全スピンは S = 0(1/2 - 1/2)となります. この状態(1S0)は一重項状態です.
一方,2個の価電子が5s軌道と5p起動にある励起状態では,スピンが逆向きの状態と同じ向きの状態が有るので,2個の価電子の全スピンは S = 0(1/2 - 1/2)または S = 1(1/2 + 1/2)となります. 前者(1P0)は基底状態と同じく一重項状態,後者(3PJ)は三重項状態です.
一般的に,一重項状態から一重項状態へ遷移する確率は高く(許容遷移),一重項状態から三重項状態(または三重項状態から一重項状態)へ遷移する確率は低くなります(禁制遷移).
Sr原子のエネルギー準位図を上記の要件と照らし合わせると,以下の様になります.
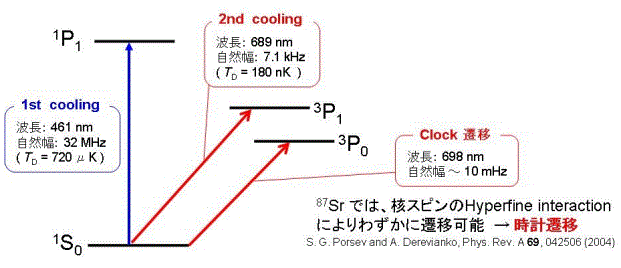
Sr原子のエネルギー準位図
(長野重夫「光周波数標準の現状と将来展望」[LINK]より)
- 1S0 ↔ 1P1(λ = 461 nm)
ΔL = ±1
ΔS = 0
ΔJ = ±1
選択則を満足するので許容遷移.
1P1 は自然幅が広い(32 MHz)励起状態である([要件3]に適合). - 1S0 ↔ 3P1(λ = 689 nm)
ΔL = ±1
ΔS = ±1
ΔJ = ±1
選択則を満足しない(ΔS ≠ 0)ので禁制遷移.
3P1 は自然幅が少し狭い(7.1 kHz)励起状態である([要件4]に適合). - 1S0 ↔ 3P0(λ = 698 nm)
ΔL = ±1
ΔS = ±1
ΔJ = 0(J = 0 → J = 0)
選択則を満足しない(ΔS ≠ 0 かつ J = 0 → J = 0)ので禁制遷移(二重禁制). ただし,87Srでは核スピンとの超微細相互作用が有るので,わずかに遷移可能.
3P0 は自然幅が非常に狭い(〜 10 mHz)励起状態である([要件1]に適合).
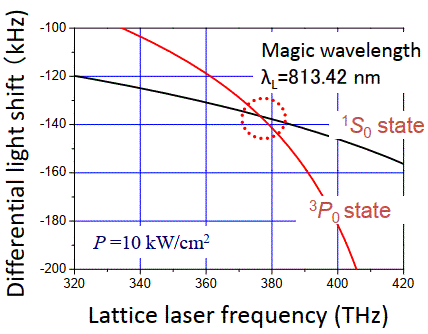
また,光格子を作るレーザ光の波長 λL を 813.42 nm 付近に設定すれば87Srの基底状態(1S0)と励起状態(3P0)のシュタルクシフトが等しくなる事が実験的に確認されています([要件2]に適合).
以上,87Srは[要件1]〜[要件4]のすべてに適合するので、光格子時計に用いる事ができます.
87Srの基底状態(1S0)と励起状態(3P0)のシュタルクシフト
(香取秀俊「光格子時計の高精度周波数比較」[LINK]より)