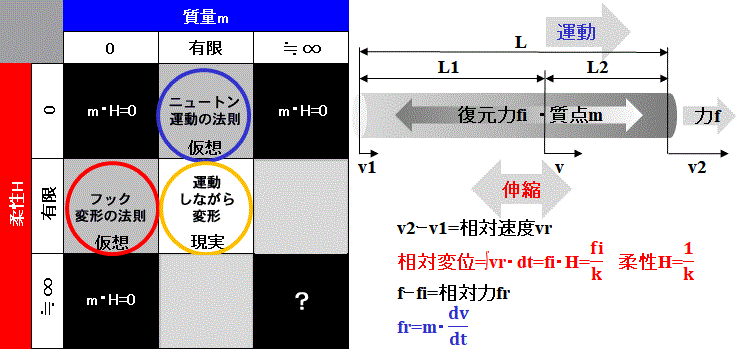
fig.7_1~7_4の右4段目の換算温度について説明する。
力学エネルギは式(1.3)に従い、速度エネルギ(外延量)と力エネルギ(内包量)の和で構成されている。
一方、熱エネルギは式(1.4)に従い、絶対零度0(k)を基準にしてそこからの温度差によって蓄える量が決まる。
これは前述のように、地球の重心からの距離=位置に応じて決まる位置エネルギと等価な物理量である。
すなわち、表1のように熱エネルギとは物質の内部で復元力が生じている時の力エネルギ=位置エネルギと同じ性質を持った内包量である。 ここで両エネルギの構成を式で表すと、
| 力学エネルギ = 外延量 + 内包量 = const. |
(1.6) |
| 熱エネルギ = 内包量 |
(1.7) |
前述のように、物質が熱エネルギを蓄えている事を力学的にバネの伸縮に置き換えて表現した。
これは上記の式(1.7)を(1.6)に置き換えたと言える。
力学エネルギは振動エネルギと言えるから万物が持っているド・ブロイ波のエネルギとも言える。
では、式(1.6)と(1.7)の両者は如何なる関係なのだろうか?
熱力学第二法則は、物質の温度変化はオーブンの中の食品のように外部から熱エネルギを供給して起こる事を示している。
ここでジュールが行った実験を振り返えると、
・断熱されている羽根車の入った水槽を用意する。
・羽根車にオモリのぶら下がった滑車を繋ぎ、オモリを所定の高さから落下させると羽根車が水を撹拌する。
・水槽の水温の変化を観測する。
ここでは水槽に外部からエネルギを供給している事になるが、これは力学的にオモリが蓄えている位置エネルギである。
オモリの落下と供に位置エネルギは逐次速度(運動)エネルギに変換されるが、オモリが最初の位置から最後の位置まで移動する区間では両エネルギの和は常に一定である。
これはエネルギ保存則と呼ばれ、式(1.6)が示している事と同じである。
ジュールは、"オモリが蓄えていた位置エネルギは水槽の水の温度を上昇させるのに必要なエネルギに等しい" なる仮説を立て、その正しさを自覚したと思われる。
この時、彼はこのエネルギを力学エネルギと区別して熱エネルギと呼んだのだろうか?
温度が変化したという現象から熱という文言が連想されるのは自然であり、我々は熱エネルギという概念を持ってはいるが、熱エネルギとは何か?を説明出来るだろうか?
熱力学なる学問が確立されているのでそれを紐解けば、さまざまな現象を説明し、課題を解決出来る。
熱力学は熱に関する理論だが、本来は必ずしも熱に関わるとは限らない式(1.3)に示されるエネルギ保存則から派生したという見方も出来る。
・熱力学第一法則はエネルギ保存則とも呼ばれるが、熱に限らずエネルギ全般に渡って成立している。
・熱力学第二法則は電気エネルギや化学エネルギについても成立している。
しかしながら、法則に熱を冠することで却って本質を見え難くしていないだろうか?
この熱なる概念は、温度という計測可能な物理量があった事で生まれたように思われる。
温度を変化させる原因としてそこにエネルギの出入りがある事は様々な実験から示されるが、ジュールが行った実験は、決して熱エネルギなる別の種類のエネルギの存在を示したものでは無い。
式(1.4)が示されたのも、実験を通して温度Tと質量mと比熱Cpに比例するという事実を示しているだけで、エネルギがそこに生じるメカニズムは不問としている。
そのような見方をすると、先述のようにエネルギとは本来、表1に示す、外延量 + 内包量の形であり、内包量単独の熱エネルギとは、課題解決の為の便宜的、あるいは実用的な見方と言える。
そして、力学エネルギを扱うには質量m、柔性Hなる対になった特性値が必要であり、これが力学の双対性と呼ばれる。
| 外延量:速度(運動)エネルギEv = 1/2 m・v2 質量mに蓄積される |
(1.1) |
| 内包量:位置エネルギ=力エネルギEf = 1/2 H・f2 柔性Hに蓄積される |
(1.2) |
ここから、換算温度とは、物質が蓄えている力学エネルギ(J)から求める温度(k)と言える。
これを計算するには、時間に対する温度変化=温度勾配(ks-1)は、同じく時間に対するエネルギ変化=パワ(Js-1)に比例する事から求められる。 但し、以下に示す注意が必要である。
ケース1を例に、区間を以下の3つに分けて考える。
・1.物質を解放してから速度変動を印加するまでの区間は式(1.3)に従ってエネルギE_SUMrは一定値を示す。
・2.次に速度変動を印加している区間では値がドリフトしている。
・3.印加終了後は再び一定値を示す。
このように捉えると、区間1、3に付いては外部からエネルギの供給が無いが、区間2は速度変動印加によるエネルギが供給されている事で区別される。
従って物質は速度変動印加によるエネルギの供給が行われている区間に限ってエネルギ(J)から温度(k)を求める事に意味がある。
これは一般的に熱力学第二法則と呼んでいるものである。
ここで供給されるエネルギとは、速度変動印加に因って起こる単位時間当たりエネルギ変化量=パワP_OPE(Js-1)であり、以下の式で表される。
P_OPE(Js-1)= 速度V_OPE・復元力F Fig.8参照
ここで留意すべきは、速度V_OPEは外延量、復元力Fは物質(バネ)内部に生ずる内包量である。
繰り返しになるが、
・パワ(Js-1)は単位時間当たりのエネルギ(J)であり、速度=外延量と力=内包量の積である。
・物質に外部から任意に印加出来るのは速度のような外延量に限られる。
・復元力Fのような内包量は人間が関与する事が出来ない。
従って人間が物質に印加したのは速度V_OPE(外延量)だが、それを受けて物質内部には柔性Hによって復元力F(内包量)が生じる事で初めて物質にパワが印加された事になるのである。
これはパワとは自分、そして相手に質量mと柔性Hが有って初めて印加出来るという意味でもある。
教科書では力について作用~反作用の原理と呼んでいる。
しかし、自分と相手、そして速度(外延量)と力(内包量)が対で揃って初めて作用~反作用の原理が成り立つと言える。
次に、換算温度は以下の手順で求められる。
・サンプリング時間:Δt(s)、初期温度:T_Ini(k)と置くと、
・ヒートマスHm(Jk-1) = m・Cp
・温度勾配dT(ks-1) = P_OPE / Hm
・換算温度T(k) = T_Ini + dT・Δt
また、エネルギ E_SUMrを用いて以下の手順でも求められる。
・パワdE(Js-1) = (E_SUMr(n) − E_SUMr(n−1)) / Δt nは計算ステップを示す。
・温度勾配dT(ks-1) = dE / Hm
注:前述のように、有効なのは区間2のみであり、仮に区間1~3まで連続してdEを求めてしまうと、1、 2そして2、3の区間が切り替わる境で巨大な値になってしまい、正しい温度勾配dtが得られない。
Fig.8に物理機能モデル上のパワと蓄えられるエネルギを示す。
左上に速度V_OPEを印加すると(バネを縮めたり延ばすと)物質の柔性Hが復元力Fを返す。
P_OPE(Js-1)= 速度V_OPE・復元力F
このパワによって物質に蓄えられるエネルギE_SUMr = 速度エネルギEv + 力エネルギEf ≠ const. となって変化する。
| 速度(運動)エネルギEv = 1/2 m・v2 |
(1.1) = 外延量 |
| 力エネルギ"力エネルギEf = 1/2 H・f2 |
(1.2) = 内包量 |
| エネルギE_SUMr = 速度エネルギEv + 力エネルギEf ≠ const. |
(1.3) = 外延量+内包量 |
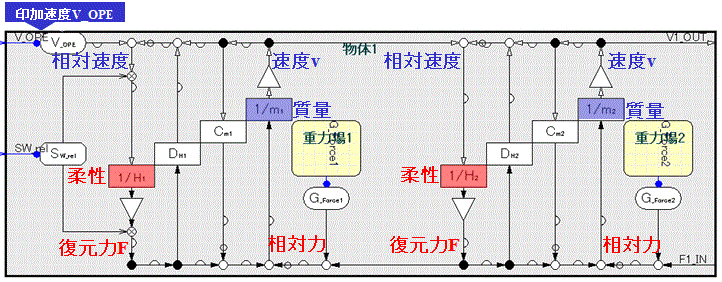
Fig.8
|