研究ノート
非線形振動は捉えどころが無い?
2025.7.21
五十川晋一
|
 はじめに
はじめに
機械工学の分野では振動現象は様々にシミュレーションが行われている。
現代のようなパソコンが普及する以前は機会は限られていた。
その時代にどんな解析が行われていたかを振り返ると、故障や事故に至った原因究明といった例が多い。
例えば、振動するエンジンが暴れないように柔らかいゴムで支持する場合の挙動解析が知られている。
こうした例は現実に起きては困るという実用的なものと言える。
一方、純粋に物理学的な事象を解明しようとする例も見られる。
振り子時計の振り子は単純な正弦波を持つ線形振動の例であるが、振り子の先にもう一つ振り子を繋げると非線形系となり、二つのオモリが描く軌跡は一気に複雑なものとなる事が知られている。
これは二重振り子と呼ばれ、軌跡はその複雑な様相からカオス軌道と呼ばれている。 補足資料4参照
振り子は正確な時を刻むための仕組みであり、わざわざ二つ繋げようという発想は興味が無ければ湧いてこない。
中には100個繋げた場合の軌跡をコンピューターで強引に解いてみた例も見られる。*1
本報では物理機能モデル手法を用いてバネの振動について、1個のバネをn分割したりn連にした場合の挙動を調べる。
原子1個をバネと見なすと、それがモル数個繋がれば原子量なる質量を持つバネとなる。
例えば純鉄Fe、55.8(g)の塊はFe原子が1モル=6.022×1023個繋がったものと見なす事が出来る。
こうした見方で非線形振動を観察すると量子力学と一般力学を橋渡し出来る。
なお、物理機能モデル手法の詳細は補足資料に示した。
*1:デジタル演算では量子化誤差があるので解は近似的なものとなり、正確な挙動は知る事が出来ない。
また、誤差が累積して計算が途中で発散して信頼がおけない結果になる事がある。
 もくじ
もくじ
●柔らかい物質について
●机上実験
・実験用モデル
・パラメータ
・試験条件
・結果
●考察
・非線形系では振幅、振動数は定まらない
・物質に蓄えられるエネルギ
・エネルギが一定に保たれる意味合い
・モーペルテュイの最小原理、フェルマーの原理
・非線形系の固有振動数について
●まとめ
●おわりに
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[1]
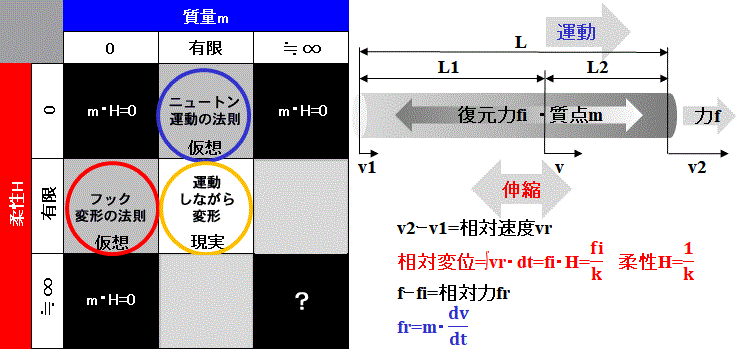
Fig.1
|
もくじへ戻る
 机上実験
机上実験
●実験用モデル
基本モデルを2連、及び7連にした例で、n連に繋げる事で任意の長さを持ったバネを表現出来る。Fig.2参照
逆に1個のバネを2分割、7分割にする事も出来る。
一端固定の場合は単体で良いが、解放したり速度を印加する場合は2連以上が必要である。
モデルは非線形系となり、波形は正弦波ではなくなる。
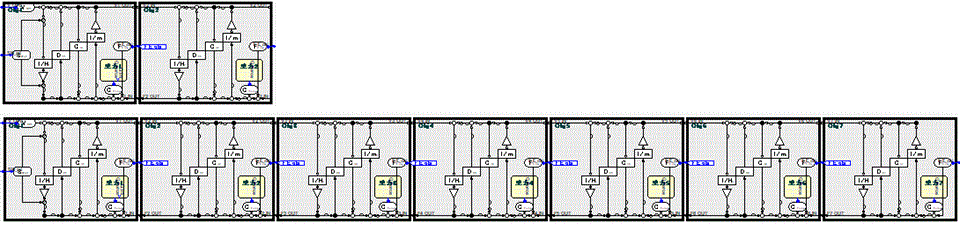
Fig.2
|
|
●パラメータ
| 表1 |
|
| 摘要 |
|
質量m(Kg) |
|
| 柔性H(mN-2) |
|
| 長さ(m) |
|
連結数 |
|
| 総質量(Kg) |
|
| 総柔性(mN-1) |
|
全長(m) |
|
| 固有振動数計算値(s-1) |
|
| 重力 |
無し |
| 温度(k) |
|
| 比熱(JKg-1k-1) |
449 Feの値を流用 |
・固有振動数計算式
・n分割の場合:f = n /(2π√(mH))
・n倍の場合:f = 1 /(2πn √(mH))
|
●試験条件
モデルは熱エネルギ等価力を印加すると伸縮を始める。Fig.3参照
バネ全長が変化する時系列波形から周期、振動数を読み取る。
・サンプリング時間:10-3(s)
・熱エネルギ等価力の印加方法は補足資料9参照
 Fig.3
Fig.3
|
|
●結果
|
Fig.4_1~2にバネ全長の時系列波形を示す。
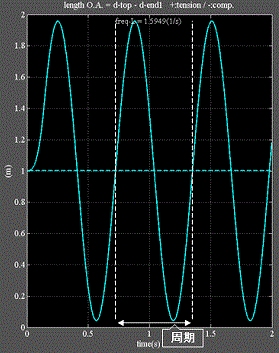
Fig.4_1 n=1=単体
・線形振動ゆえに正弦波である。
・白破線は1周期の区間を表す。
|
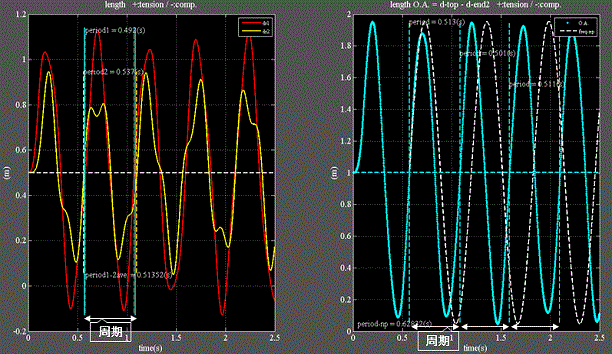
Fig.4_2 n=2分割
・非線形振動となり、正弦波では無くなる。
・左図に赤:バネ1、黄:バネ2の長さを示す。
・右図に水色:全長を示す。
・比較の為に固有振動数計算値を基に作成した正弦波を白鎖線で重ねている。
・水色は白破線より周期、及び振幅が短く、かつ一定ではない。
|
Fig.5_1~2にリサージュ波形を示す。
・左図はx軸:バネ端部速度、y軸:バネ復元力に取ったものである。
・楕円の面積はバネに蓄えられているエネルギに等しい。
・外接する双曲線は端部速度×復元力=パワを示す。
・右図はZ軸:時間軸を加えた3D表示である。
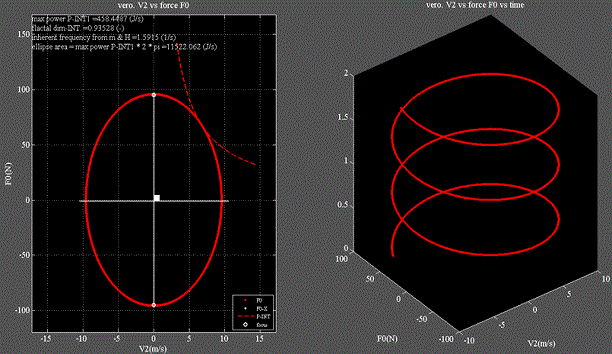
Fig.5_1 n=1=単体
・線形振動のリサージュ波形は完全な楕円形を示す。
・数学的にはsin2 + cos2 = 1を表している。
|
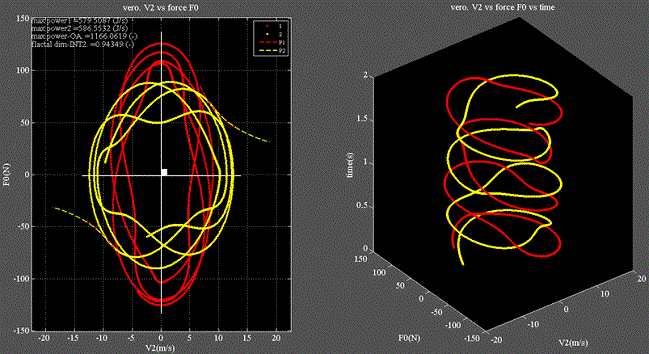
Fig.5_2 n=2分割
・非線形振動の場合、軌跡は始点から終点まで決して重ならない。
・固定側のバネ1と解放側のバネ2はお互いに位相が90度=π/2ズレる。
・楕円にはならないので、バネ1、2の各エネルギは時々刻々変化している事になる。
・これは二重振り子の軌跡に見られるカオス軌道と同じである。 補足資料4参照
|
Fig.6_1~2にバネに蓄えられているエネルギの時系列波形を示す
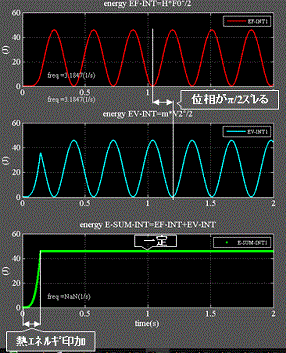
Fig.6_1 n=1=単体
・左上:力エネルギ式(1.2)を示す。 線形振動ゆえに正弦波である。
・左中:速度エネルギ式(1.1)を示す。 線形振動ゆえに正弦波である。
・左下:緑線:力エネルギ+速度エネルギを示す 式(1.3)、熱エネルギ印加後は一定を示す。
・これは力エネルギと速度エネルギは位相がπ/2ズレているからである。
・数学的にはsin2 + cos2 = 1を表している。
|
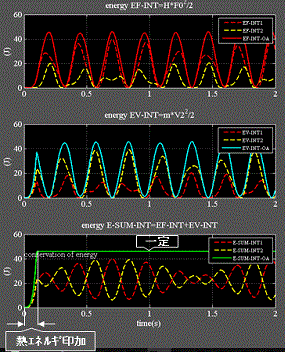
Fig.6_2 n=2分割
・左上:力エネルギ式(1.2)を示す。 赤破線:バネ1、黄破線:バネ2 赤実線:両者の和
・左中:速度エネルギ式(1.1)を示す。 赤破線:バネ1、黄破線:バネ2 水色実線:両者の和
・左下:緑線:力エネルギ+速度エネルギを示す 式(1.3)、熱エネルギ印加後は一定を示す。
・バネ1、2の各エネルギは非線形振動ゆえに正弦波ではなく複雑に変化するが、その和=緑線は常に一定となる。
|
Fig.7_1~3にn=7分割の例を示す。
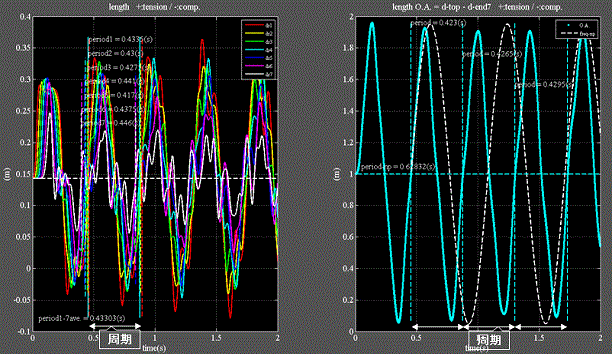
Fig.7_1 時系列波形
・左図にバネ1~7の全長を、赤、黄、緑、水色、青、紫、白線で示す。
・個々のバネの長さは個別に変化する。
・右図に水色:全長を示す。
・比較の為に固有振動数計算値を基に作成した正弦波を白鎖線で重ねている。
・水色は白破線より周期、及び振幅が短く、かつ一定ではない。
|
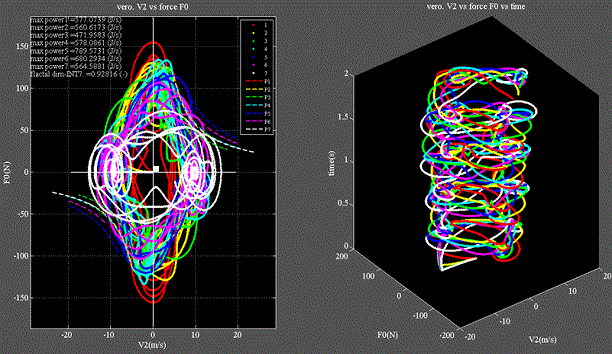
Fig.7_2 リサージュ波形
・バネ1:赤に対し、バネ2~7は時計回りに少しずつ位相がズレて行き、最後の7:白は90度=π/2ズレる。
・楕円にはならないので、バネ1~7の各エネルギは時々刻々変化している事になる。
|
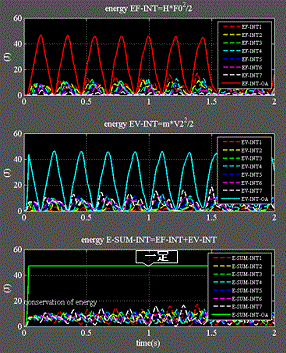
Fig.7_3 エネルギ波形
・左上:バネに蓄えられる力エネルギを示す。式(1.2) 赤~白破線:バネ1~7 赤実線:総和
・左中:バネに蓄えられる速度エネルギを示す。式(1.1) 赤~白破線:バネ1~7 水色実線:総和
・左下:緑線:力エネルギ+速度エネルギを示す 式(1.3)、熱エネルギ印加後は一定を示す。
・バネ1~7の各エネルギは複雑に変化するが、その総和=緑線は常に一定となる。
|
|
もくじへ戻る
 考察
考察
●非線形系では振幅、振動数は定まらない
Fig.4_1~2で時系列波形を観察すると線形振動は正弦波ゆえに時間の経過に左右されず、各周期毎の波形は変化しない。
一方、非線形振動の波形は時々刻々複雑に変化し、各周期毎に振幅と周期が一定では無く、振動数は定まらないと言える。
次にFig.5_2、Fig_7_2のリサージュ波形を観察すると軌跡は決して重ならない。
これは一見、予測不能に見えるが再現性があるのでランダムではない。
こうした性質は数学的にはフラクタル=自己相似と呼ばれる。
|
●物質に蓄えられるエネルギ
物質全般は絶対零度以上の温度にあるとき、熱エネルギを蓄え、かつ伸縮している。 *2
まず、伸縮している物質の力学的エネルギEは以下のように定義される。
| Ev = 1/2 m・v2 |
Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.1) |
| Ef = 1/2 H・f2 |
Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.2) |
| E = Ev + Ef = const. |
|
(1.3) |
上式は力学の双対性を現し、式(1.3)は対になったエネルギの和は常に一定となる事から、伸縮する物質に限ったエネルギ保存則と呼べる。補足資料1参照
ここで、エネルギを振動数f、振幅A で表すと、
| エネルギE = 2π2 m・f2・A2 f:振動数、A:振幅 |
(1.4) |
次に、物質は絶対零度 0(k)=(-273.15℃)以上で熱エネルギEtは以下のように定義される。
| Et = m・Cp・T Et:熱エネルギ、m:質量、Cp:比熱、T:温度 |
(1.5) |
*2:ド・ブロイの物質波と言え、物質全般はバネと見なす事が出来る。
ここでFig.6_1~2でエネルギ波形を観察すると、式(1.3)が示すエネルギの総和だけはリサージュ波形のバネ端部速度と復元力が互いにどんな軌跡を描こうとも、常に一定に保たれている事が判る。
また、n分割してもエネルギは不変である。(n連の場合はエネルギはn倍となる)
そして、エネルギ一定ゆえに式(1.4)より振動数fと振幅Aはお互いに反比例の関係を保ちながら常に変動すると言える。
|
●エネルギが一定に保たれる意味合い
ここで、生命体の細胞分裂を考える。
光合成を行なう植物の場合、それに必要なエネルギ原資は光エネルギである。
光エネルギの摂取と細胞分裂で消費されるエネルギ収支が一定であれば、安定して細胞分裂が繰り返される筈である。
但し、細胞の長さが常に同じ比率で分裂が起きればいずれ枝葉同士は重なり合い、光を受ける部分と影になる部分が生じて生育が妨げられる。
あるいは、重力下では根元の部分は先端が細胞分裂する度に増加する質量を支え切れずに折れてしまう。
従って、その比率は漸減してゆかねばならない。
これにより枝葉は螺旋形を描いて分岐する事になり、光エネルギを植物全体で満遍なく摂取出来る。補足資料5参照
これは種の保存の仕組みと言える。
このように考えると数学的なフラクタル=自己相似とは、Fig_6_2、Fig.7_3が示すようにバネを何分割にしようと系全体のエネルギは常に一定に保たれる=力学的なエネルギ保存則に通じるように思われる。
|
●モーペルテュイの最小原理、フェルマーの原理
・モーペルテュイの最小原理:力学系の運動はエネルギ*3 を最小にするような軌道に沿って実現される。(1747年)
・フェルマーの原理:光は光学的距離が最短になる経路を通る。(1661年)
この両原理についてもエネルギ保存則に通じる部分があるように思われる。
但し、この二つの原理は片や粒子(運動)、片や波動(変形)を対象にしており、物理機能モデルでは運動と変形は切り離せないという見方をしている点で相違がある。
補足資料に示したモデル図が示すように、速度と力、運動と変形が循環する=ループになっているのである。
そのおかげでエネルギは常に一定に保たれるのである。
これを数学的に示したのが補足資料1であり、エネルギ=面積を定めればどのような楕円軌道でも描けるという事である。
この事は逆に粒子(運動)と波動(変形)を切り分けた時にモーペルテュイの最小原理、フェルマーの原理は成り立つと言える。
ド・ブロイは ”物質は粒子でもあり波動でもある” と言う物質波(1924年)の概念に辿り着く過程で、モーペルテュイの原理は物質を粒子として扱い、フェルマーの原理は光を波動として扱っているが、二つの原理は同一であると解釈している。
物質波とは式(1.5)によって温度=熱エネルギが定まれば、その軌道は無限に存在する(定まらない)という性質を持っていると言える。
*3:当時は、”作用と呼ばれる汎関数“ と表現されていたが、エネルギという概念が未だ確立されていなかった。
エネルギの概念が確立されるのは19世紀後半である。
|
●非線形系の固有振動数について
非線形系では振幅、振動数は定まらないので固有振動数なる言い方は出来ないかもしれない。
ここで、Fig.4_1~2に示した一周期目の観測周期を例にモデル連結数と振動数の関係を確認した結果をFig.8に示す。
・分割数、及び連結数nを1~7まで振ってみたものである。
・x軸:n数、y軸:固有振動数計算値に対する観測値の比率を取る。
・赤:n分割にした場合、黄:n倍にした場合である。
・n=1=単体の場合、観測値と固有振動数計算値は一致する。
・モデルをn分割にしてもn倍しても観測値は固有振動数計算値より高くなる事が判る。
・n数を増やして行くと比率は単調増加ではなく、ある値に漸近して行くように見える。
・これはある任意の座標から原点(0,0)に限りなく漸近する螺旋の性質と同じと言える。Fig.9参照
・螺旋はフラクタルの一部であり、螺旋の集合もまたフラクタルとなる。補足資料5参照
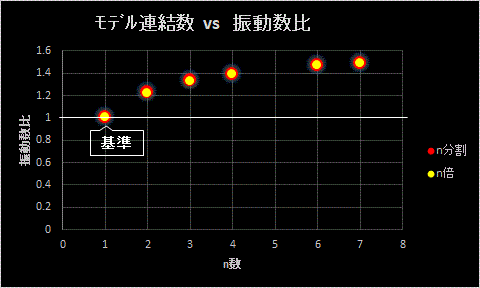
Fig.8
|
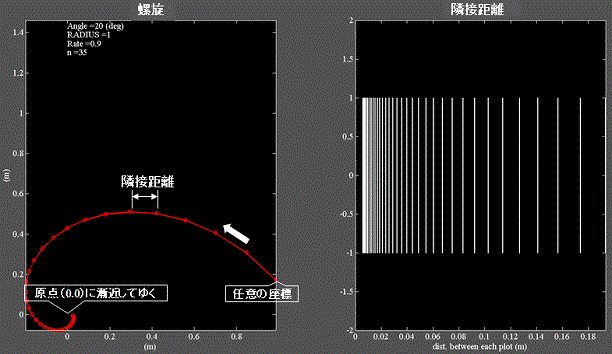
Fig.9 螺旋の事例
・左図:XY座標上の任意の点から螺旋を描くと原点(0.0)に漸近してゆく。
・右図:各プロット間の隣接距離をバーコード様に表示したものである。
・原点に近づくにつれてプロットはお互いに接近するがプロット数を増やしても隣接距離は決して0にはならない=重ならない。
|
ところで、Fig.8に示した固有振動数計算値に対する観測値の比率だが、n=1=バネ単体の1に対し、n≧2では1.22~1.48と無視できないオーダーである。
振動を伴う機械の設計に於いて、固有振動数計算値より実際の振動数はこのように大きいのだろうか?
大きいのだが、実害が無いのである。
この理由を説明する。
・力学的に以下のルールが存在する。
・物質=バネの一端が固定されている場合はn=1=バネは単体と見なせる。
・一端が固定されていない=浮遊している場合、または一端に速度を印加する場合はn≧2と見なさなければならない。
・理由は、後者はバネの左端と右端は独立に変位するが、1個のバネでは変位量は一つしか求められないからである。
Fig.10参照
現実界に於いて振動を伴う機械は、柔らかく変形するバネの一端は完全剛体と見なせる部材に固定されているからである。
つまり、空中に浮遊しながら伸縮するような機械は殆ど存在しない=機械として充分な機能が果たせないからである。
空中で伸縮しながら運動する物質の挙動をシミュレーションする課題は、既研究ノート浮遊する柔らかい物質の振動解析を参照されたい。
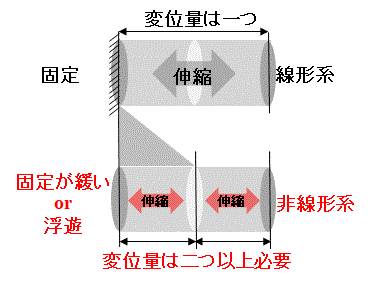
Fig.10
|
|
もくじへ戻る
 まとめ
まとめ
| ・ |
物理機能モデル手法を用いてバネをモデル化する事により以下の知見が得られる。
|
| ・ |
n=1=バネ単体の場合は線形振動である。
|
| ・ |
n≧2では非線形振動である。
|
| ・ |
線形振動系では振動数の観測値は固有振動数計算値に等しい。
|
| ・ |
非線形振動系では振動数、振幅は常に変化し、定まらない。
|
| ・ |
バネが蓄えるエネルギについてはn分割してもn倍にしても常に一定を保つ。
|
| ・ |
バネをn分割にしても、n個繋げても振動数は固有振動数計算値より高くなる。
|
| ・ |
n数を増やしてゆくと振動数はある値に漸近してゆく。
|
| ・ |
力学に於ける非線形振動系の性質は数学的にはフラクタル=自己相似と呼ばれる。
|
| ・ |
数学的なフラクタルとは物理学的なエネルギ保存則と同じである。
|
もくじへ戻る
 おわりに
おわりに
1個のバネ単体は線形振動系と述べた。
しかしながらそのバネが純Fe製ならFe原子1個が無数に連なったバネの筈である。
従って、我々が現実界で扱えるバネは全て非線形振動系という事になる。
ド・ブロイの言葉を借りるなら、万物は非線形振動系である。
これは量子力学的な見方と言える。
そう考えるならば、バネを用いた機械を設計する際に計算した固有振動数とは近似的なものという事になる。
実害が無ければそれでも良い筈である。
ニュートンは現実界は非線形系ながら、近似的に線形と見なす事で大成功を納めたと言える。
これは一般力学的な見方と言える。
フラクタルなる性質は植物に限らず、動物、地形、自然現象、あらゆるところに現れる。
判りやすい例は、自動車のサスペンションは乱暴な運転をしない限り、底付きしないように設計されている。
お互いに重ならない、干渉しないという仕組みは現実界で上手く事を運ぶ為のルールと言えよう。
"北ニケンクヮヤソショウガアレバツマラナイカラヤメロトイヒ"
これは雨ニモマケズの一節だが、宮沢賢治も認識していたように思える。
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年
・研究ノート 浮遊する柔らかい物質の振動解析 五十川晋一 著 2025年
・研究ノート 力学の双対性から見たプランク定数 五十川晋一 著 2025年
・研究ノート ド・ブロイ波の力学的解釈 五十川晋一 著 2025年
・研究ノート 力学の双対性から見たプランクの公式の導出 五十川晋一 著 2025年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 物質の柔性が粒子と波動性に及ぼす影響
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート 電子レンジの物理モデル化
研究ノート パウリの排他原理のモデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 





















