研究ノート
力学の双対性から見た超伝導現象
2025.8.1
五十川晋一
|
 目的
目的
超伝導は電磁気学上の現象だが、温度を絶対零度付近まで降下させると導体中の電気抵抗がゼロとなり、回路に電圧を印加するのを止めても電流が流れ続ける、と説明されている。
力学の双対性から、電磁気学上の現象と力学上の現象は相似と言われている。[1]
電磁気学は 実体の無い“場の学問” と言われているが、力学はニュートン力学に代表される “実体を対象にした学問”と言える。
筆者は力学の双対性を踏まえた物理機能モデル手法で作成した柔らかい物体のモデルを用いて様々な現象を観察している。
本報では超伝導現象を実体がある力学上の現象に置き換えて解釈を試みる。
なお、物理機能モデル手法の詳細は補足資料に示した。
 もくじ
もくじ
●柔らかい物質について
●エネルギの印加について
●机上実験
・実験用モデル
・パラメータ
・試験条件
・結果
●考察
・物質に蓄えられるエネルギ
・導体とバネの相似性
・力学と電磁気学の相似則
・内包量と外延量について
・導体が伝えているものは何か?
・導体の伝播速度とは?
・粘性抵抗発現のメカニズム
・マイズナー効果の解釈
・電気抵抗の物理的メカニズム
●まとめ
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[2]
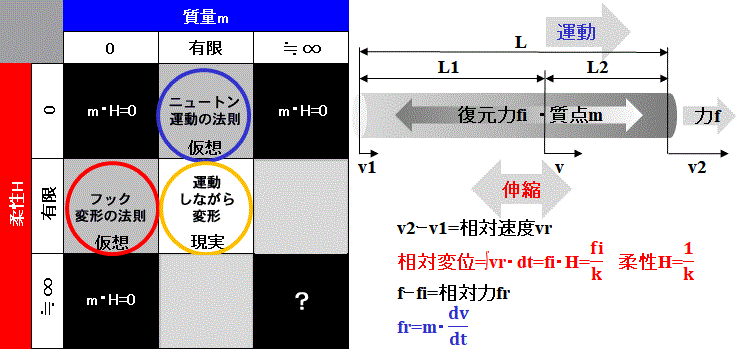
Fig.1
|
もくじへ戻る
 エネルギの印加について
エネルギの印加について
エネルギの印加のわかり易い事例をFig.2に示す。
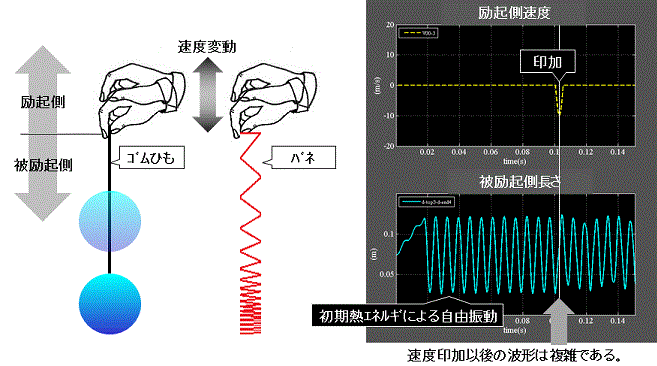
Fig.2
|
水ヨーヨーはゴムひもの端を持って上下に振るが、振り方によって大きく振らす事が出来る。
水ヨーヨーの隣のバネは、同様に縁日で良く見かける玩具を示している。
このバネの元祖はSLINKYと呼ばれ、米国で1945年に玩具として登場し、その亜流が世界中に流布している。
SLINKYの遊び方は様々だが、水ヨーヨーと同じような遊び方が本報の例である。
遊びの中で無意識のうちに振るタイミングや周期を合わせている訳である。
逆にタイミングと周期を故意に合わせなければ、手を振ってもヨーヨーやバネを殆ど振らさない事も出来る。
エネルギの印加とは水ヨーヨーやバネ自身が蓄えているエネルギに対して外部から追加したり、逆に吸収する事であり、物質が励起された、または去勢されたという言い方も出来る。
物質全般は絶対零度以上の温度にあるとき、熱エネルギを蓄え、かつ伸縮している。 *1
まず、伸縮している物質の力学的エネルギEは以下のように定義される。
| Ev = 1/2 m・v2 |
Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.1) |
| Ef = 1/2 H・f2 |
Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.2) |
| E = Ev + Ef = const. |
|
(1.3) |
上式は力学の双対性を現し、式(1.3)は対になったエネルギの和は常に一定となる事から、伸縮する物質に限ったエネルギ保存則と呼べる。補足資料1参照
次に、物質は絶対零度 0(k)=(-273.15℃)以上で熱エネルギEtは以下のように定義される。
| Et = m・Cp・T Et:熱エネルギ、m:質量、Cp:比熱、T:温度 |
(1.4) |
熱エネルギEtは同じ内包量*2である力エネルギEfに変換出来るので、Et = Ef = 1/2 H・f2 の関係から力fが求められる。
この力fを最初に被励起側のバネに印加しておくことで、物質が熱エネルギを蓄えている事を力学的にバネの伸縮に置き換えて表現する事が出来る。
*1:これは量子力学的な視点から出発したド・ブロイの物質波の考え方であるが、現実的にはその振動エネルギは微弱であり、観測可能なオーダーとは言えない。
熱エネルギを持って振動していると言っても、水ヨーヨーやSLINKYのように相対的に伸縮の振幅が大きければその振動は埋もれてしまい、知覚出来ないと言う意味合いである。
*2:内包量については考察で触れる。
もくじへ戻る
 机上実験
机上実験
●実験用モデル
下図は一次元方向に伸縮する物体を模擬したモデルの一例であり、バネと考えて差し支えない。
基本モデルを6連(2連×3)にしたもので、n連に繋げる事で任意の長さを持ったバネを表現出来る。
このモデルは電磁気学的には送電線のような導体に相当する。

Fig.3
|
|
●パラメータ
・質量m:1.0(kg)×6
・柔性H:1.0e−8(mN−1)×6 (剛性kの逆数)
・長さL:0.1(m)×6
・粘性抵抗係数Cm:0.2(Nsm−1)
・比熱Cp:435(JKg-1k-1) (鉄の値を流用)
・初期温度:273.1(k)= 0(℃)、及び絶対零度 = 0(k)=-273.15(℃)の2水準
・環境温度:273.1(k)= 0(℃)、及び絶対零度 = 0(k)=-273.15(℃)の2水準
・重力:0=無重力下とする
|
●試験条件
・サンプリング時間:10-5(s)
・物質に初期熱エネルギを印加して自由振動させる。 印加方法は補足資料9参照
・既定の時刻に以下の速度を印加する。Fig.4参照
・目標速度:1(ms−1)
・加速度:50(ms−2)
・目標速度に達したら印加を止める、及び継続するの2ケースとする。
・なお、物質は熱伝達の無い断熱条件下とする。
 Fig.4
Fig.4
|
|
●結果
|
Fig.5_1~4に各物理量の時系列波形を示す。
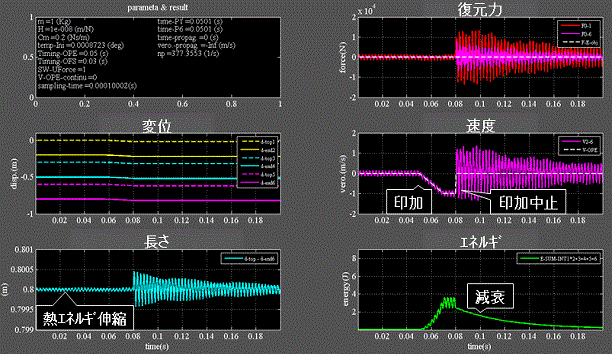
Fig.5_1 速度印加 0℃
・左下段:バネは温度に応じた熱エネルギ伸縮を伴う。
・左中、下段:バネの一端に速度を印加すると伸縮しながら移動し始める。
・右上、中、下段:印加を止めるとバネは停止し、粘性抵抗により速度、復元力は減衰する。
・右下段:バネに蓄えられるエネルギも減衰する。
|
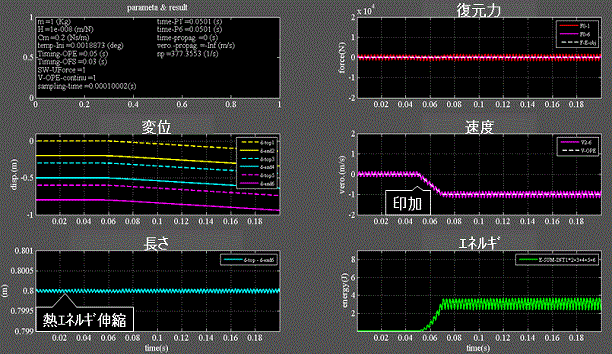
Fig.5_2 速度印加継続 0℃
・左下段:バネは温度に応じた熱エネルギ伸縮を伴う。
・左中、下段:バネの一端に速度を印加し続けると粘性抵抗に抗して伸縮しながら移動し続ける。
・右下段:バネに蓄えられるエネルギは維持される。
|
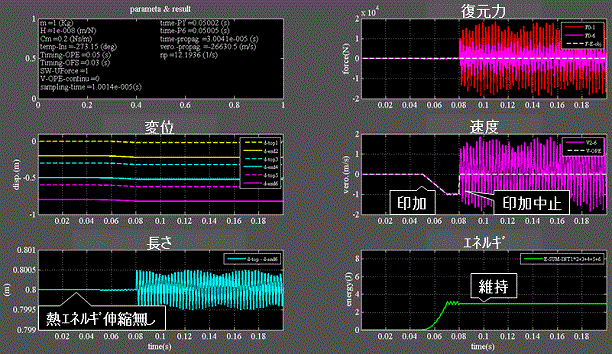
Fig.5_3 速度印加 絶対零度 = -273.15℃
・左下段:バネは熱エネルギ伸縮を伴わない。
・左中段:バネの一端に速度を印加すると伸縮しながら移動を始める。
・左中、下段:印加を止めると粘性抵抗が働かないのでバネは停止するが伸縮し続ける。
・右上、中段:速度、復元力はゼロを中心に変動を続ける。
・右下段:バネに蓄えられるエネルギは維持される。
|
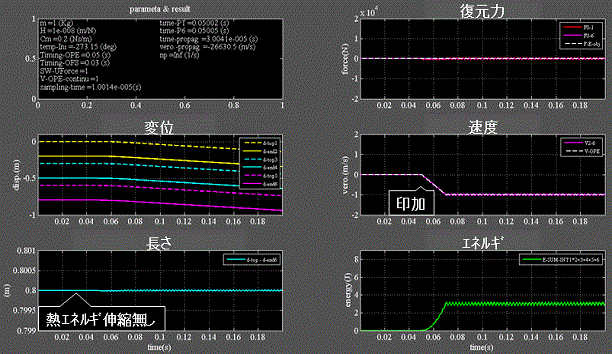
Fig.5_4 速度印加継続 絶対零度 = -273.15℃
・左下段:バネは熱エネルギ伸縮を伴わない。
・左中、下段:バネの一端に速度を印加し続けると伸縮しながら移動し続ける。
・右下段:バネに蓄えられるエネルギは維持=保存される。
|
Fig.5_5~8にパワ、エネルギ、温度の時系列波形を示す。
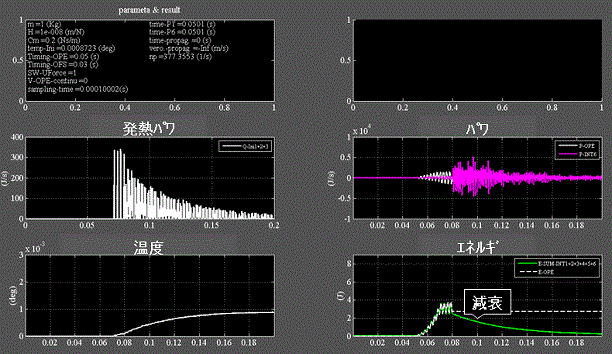
Fig.5_5 速度印加 0℃
・右下段:印加したエネルギ(白)に対してバネに蓄積されるエネルギ(緑)は減衰してしまう。
・左中段:粘性抵抗に因って消費されたエネルギが熱エネルギに変換される。
・左下段:温度が上昇する。
|
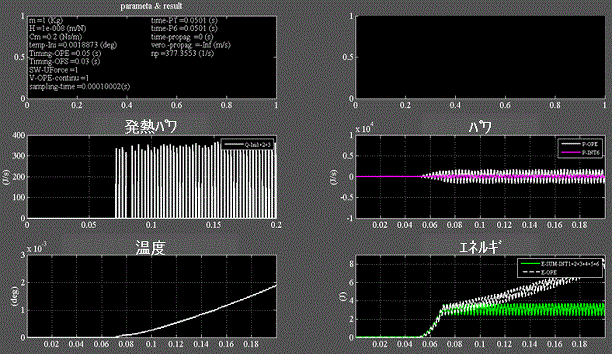
Fig.5_6 速度印加継続 0℃
・右下段:印加するエネルギ(白)はバネに蓄積されるエネルギ(緑)より大きい=粘性抵抗に抗する分だけ多く必要。
・左中段:粘性抵抗に因って消費されたエネルギが熱エネルギに変換される。
・左下段:温度は雰囲気温度と釣り合うところまで上昇し続ける。
|
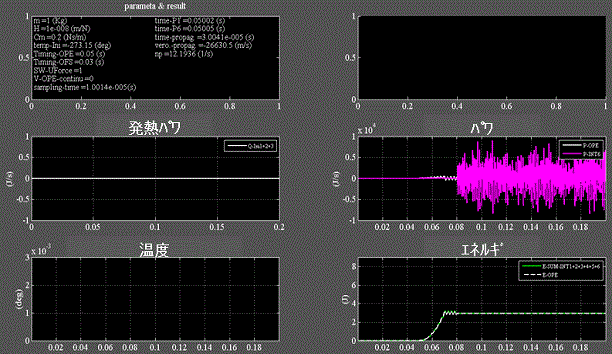
Fig.5_7 速度印加 絶対零度 = -273.15℃
・右下段:印加したエネルギ(白)はバネに蓄えられるエネルギ(緑)に等しい=重なっている。
・左下段:粘性抵抗が働かないので温度上昇はない。
|
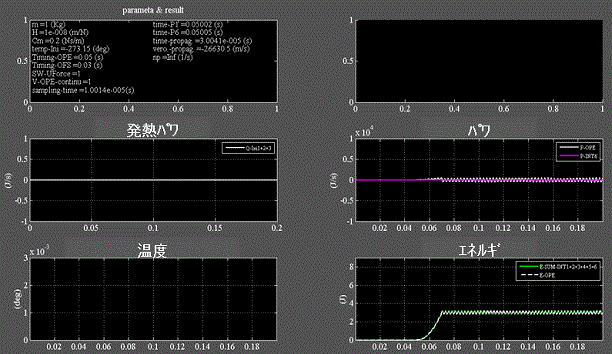
Fig.5_8 速度印加継続 絶対零度 = -273.15℃
・右下段:印加したエネルギ(白)はバネに蓄えられるエネルギ(緑)に等しい=重なっている。
・左下段:粘性抵抗が働かないので温度上昇はない。
|
以下に結果を要約する。
| 絶対零度以上 | 絶対零度 |
バネは温度に応じた熱エネルギ伸縮を伴う
↓
バネの一端に速度を印加すると伸縮しながら移動し始める
↓
バネの温度が上昇する
↓
印加を止めるとバネは停止する
↓
粘性抵抗により伸縮は減衰して止まる
|
バネは熱エネルギ伸縮を伴わない
↓
バネの一端に速度を印加すると伸縮しながら移動し始める
↓
バネの温度は上昇しない
↓
印加を止めるとバネは停止する
↓
粘性抵抗が働かないので伸縮し続ける
|
|
もくじへ戻る
 考察
考察
●物質に蓄積されるエネルギについて
本実験はバネを振る=一端に速度を印加するにはエネルギを必要とし、そのエネルギがバネ自身で蓄えているエネルギに加算される様子を示している。
このエネルギは速度を印加したのだから速度(運動)エネルギと考えがちだが、物質がバネのように柔性Hを持って伸縮する場合、力(変形)エネルギも同時に蓄える事を理解しなければならない。
この見方をする時に、式(1.3)が成り立つ。
これが力学の双対性の一つの側面である。
もし、伸縮しない=柔性=0=完全剛体と見なす場合は力(変形)エネルギは蓄える事が出来ず、速度(運動)エネルギのみとなり、式(1.3)は成り立たない。
あらためて記述すると、
・物質に外部から速度を印加すると速度エネルギが印加されるだけではない。
・バネ自身の内部に復元力が生じるので同時に力エネルギも印加された事になる。
なお、速度印加のタイミングがバネが伸び過程か、縮み過程かによってエネルギは加算だけでなく減算になる事がある。
これは水ヨーヨーやバネを振るタイミングが悪ければ思ったように振れないという事に相当する。
この詳細については既研究ノート浮遊する柔らかい物質の振動解析を参照されたい。
ところで、この仕組みは普段の生活や社会の中でも見られるのではないだろうか?
・人に指示したのに、こちらが思ったように動いてくれない。
・企業に投資したのに見返りが思ったほど大きくない。
これは指示された人の脳には感情が湧き、投資した企業の内部には反応が興るが、それが見えないからではないだろうか?
双対性とは力学だけに限らない、あるルールがあるように思える。
次の内包量と外延量についてをお読み頂きたい。
|
●内包量と外延量について
補足資料3参照
ここに示されている重要なルールをあらためて以下に示しておく。
・人間が操作出来るのは外延量のみであり、内包量については関与出来ない。
|
●導体とバネの相似性
A→B地点へ送電線で電力を供給する場合、導体には電気抵抗があるのでA地点で印加した電圧はB地点では降下する。
その降下分を少なくして送電効率を上げる方法として、導体を絶対零度近くまで冷却するというアイデアがある。
冒頭の "エネルギの印加について" で触れたように、絶対零度以上の温度では物質は熱エネルギを蓄えて振動している。
従来、見られるのは以下のような説明である。
・導体内で電子が移動して電流が流れる際、電子は振動する原子に邪魔されながら進もうとするので抵抗を受ける。
・これが電気抵抗となって現れる。
ならば、温度を絶対零度まで下げれば導体内の原子、電子の振動は停止し、電子はスムーズに流れる、と言う推論は頷けるし、実験によって確められている。
しかしながら、原子、電子が振動するとしてもその振動の仕方、そして電子の移動を邪魔するメカニズムについては未解明である。
本報では実体を伴ったバネを用いて挙動が容易に観測出来るようにした訳だが、これは冒頭で述べたように、力学と電磁気学の相似則が証になっている。
|
●力学と電磁気学の相似則
|
補足資料に掲載した力学と電磁気学の相似則の表から抜粋する
・速度v vs 電圧V
・力f vs 電流I
・粘性抵抗係数Cm vs コンダクタンスG=1/電気抵抗係数R
・質量m vs コンデンサの静電容量C
・柔性H=1/剛性k vs コイルのインダクタンスL
・速度(運動)エネルギ vs 静電エネルギ
・力(変形)エネルギ vs 電磁エネルギ
・質量mは速度(運動)エネルギを蓄積する vs コンデンサの静電容量Cは静電エネルギを蓄積する
・柔性Hは力(変形)エネルギを蓄積する vs コイルのインダクタンスLは電磁エネルギを蓄積する
・速度v×力f vs 電圧V×電流A いずれも瞬時エネルギ(w)=パワ、仕事率である
(パワを時間積分すればエネルギ(wh)となる。 1(wh)=3600(J))
・粘性抵抗係数Cm ×(速度v)2 vs コンダクタンスG ×(電圧V)2 いずれも瞬時エネルギ=発熱量である
ここで重要なのは、粘性抵抗係数CmとコンダクタンスG=1/電気抵抗係数Rの関係である。
Cm、G、Rとは外延量→内包量、あるいは内包量→外延量に変換する際の変換係数であるという事である。
|
粘性抵抗係数Cm |
コンダクタンスG=1/R |
電気抵抗係数R |
| 物理的機能 |
速度→力に変換 |
電圧→電流に変換 |
電流→電圧に変換 |
| 抵抗される相手 |
速度 |
電圧 |
電流 |
以上を踏まえ、本報のバネモデルによる試験に於いて得られた知見をまとめると、
・速度印加前には温度に応じてバネに蓄えられるべき熱エネルギEtを印加済である。
・その時点でバネは自由振動=伸縮を始めている。
・バネの一端に速度を印加する操作は、導体に電圧Vを印加する事に相当する。
・バネの速度印加を止めると粘性抵抗によってバネの伸縮と移動は減衰して止まる。
・熱エネルギEtに応じたバネの伸縮に加え、左端に速度を印加した事による復元力の発生→瞬時エネルギが加算される。
・バネの伸縮によって両端間に生まれる速度差は粘性抵抗によって熱エネルギEtに変換される。
・その熱エネルギEtによってバネ自身の温度が上昇する。
・これは導体やニクロム線が熱を持つ事に相当する。
・粘性抵抗が発現しない絶対零度では速度印加を止めるとバネの移動は止まる。
・一方、加算された瞬時エネルギに因って伸縮は続く。
・これは導体の場合、"絶対零度下では電気抵抗が無くなり電流が流れ続ける" と表現される事に相当する。
以上から、実験用モデルによって導体とバネの相似性が確認出来た事になる。
相違点を挙げるなら、無重力下でバネ左端に速度を印加し続ければ伸縮しながら移動を続けるが、導体は移動しない。
|
●導体が伝えているものは何か?
|
ここでバネと導体を対比してみる。
| バネ | 導体 |
バネの一端に印加した速度はバネの単位区間を撓ませる
↓
柔性Hは復元力を返す
↓
単位区間の質量mは復元力を受けて加速度を返す
↓
バネの単位区間に速度差が生じる
↓
バネの一端に印加中の速度と単位区間の速度差の合算は単位区間を撓ませる
↓
|
導体の一端に印加した電圧は単位区間の電子を撓ませる
↓
インダクタンスLは復元力を返す
↓
単位区間の静電容量Cは復元力を受けて加電圧を返す
↓
導体の単位区間に電位差が生じる
↓
導体の一端に印加中の電圧と単位区間の電位差の合算は単位区間の電子を撓ませる
↓
|
単位区間内の循環とは、
・バネ:物質自身に備わった柔性Hと質量mによる共振力学系と見なす事が出来る。(通称バネ・マス系)
・導体:電子自身に備わったインダクタンスLと静電容量Cによる共振回路系と見なす事が出来る。(通称L・C回路)
| バネ | 導体 |
| 伝えているもの | 速度×力=瞬時エネルギ=パワ | 電圧×電流=瞬時エネルギ=パワ |
| 伝播の様式 | 実体のある空間(質量場・バネ場)の疎密波 | 実体の無い空間(電場・磁場)の疎密波 |
| メカニズム | 共振力学系=バネ・マス系の連鎖 | 共振回路系=L・C回路の連鎖 |
電磁気学的に電流が流れるとは力学的には電子が移動するのではなく、単位区間の共振回路がパワを疎密波の形で伝播していると言った方が正しい。 なお、
・単位区間とはFig.2で示したn連バネの夫々の要素の事である。
・復元とは今起きたエネルギ変化から元の安定状態に戻ろうとする過程であり、エネルギ保存則の本質と言える。
・加速度と対になる加電圧とは時間に対する電圧の勾配(Vs-1)という意味である。
|
●導体の伝播速度とは?
|
伝搬しているのはパワだが、本報のバネモデルを用いてその伝播速度を以下の手順で求めてみる。
・time_P1:バネ左端に速度を印加してパワがゼロから立ち上がる時刻(s)
・time_P6:バネ右端のパワがゼロから立ち上がる時刻(s)
・L:左端~右端までの距離(m) 注:これは伸縮=変動する
・Vp:伝搬速度 = L / (time_P6 − time_P1)
・Vp = 26630.5(ms-1) と言う結果が得られた。
音速が340(ms-1)であるからそのざっと78倍というオーダーである。
導体中を電流が流れる速さは光速≒30万(Kms-1)に等しいと言われているが、実体のあるバネはこの程度のオーダーなのかもしれない。
柔性Hが小さい=剛性が高いほど伝搬速度は上がってゆく。
なお、伝搬速度が光速に達する柔性Hの推定については既研究ノート 光速に関する考察 を参照されたい。
あらためて述べるが、導体内を電子が移動する速度ではなく、疎密波によるパワの伝播速度である。
これは導体中に存在する無数の電子同士の玉突き現象(ニュートンのゆりかご)に喩えられる。 [3] Fig.6参照
物質の内部でパワが伝搬されるには柔性H=0の完全剛体ではなく、柔らかい=柔性(弾性)を持っている必要がある。
ここから電子のような素粒子は完全剛体ではなく、伸縮する=大きさ~長さを持っていると見なす必要がある。
関連するテーマとして既研究ノート ド・ブロイ波の力学的解釈を参照されたい。
ところで送電線(発電所)というゲームがあるが、これも人間を1個の電子に喩えた共振回路系の連鎖と言える。
・鬼を一人決める。
・数人で両手を繋いで車座となる、鬼は車座の中に立つ。
・車座の中から親(発電所)を決め、左右どちらかの隣の人の手を鬼に気付かれないように握る。
・握られた人は反対側の手を握れば電流となって車座を循環する。
・鬼は、今、電流を隣に伝えようとしている人を当てる。
・当てられた人は鬼を交代する。
これは手の握力で信号を伝播するゲームと言えるが、その伝搬速度が想像以上に速い事である。
伝搬速度を競うゲームも面白いかもしれない。

Fig.6
|
|
●粘性抵抗発現のメカニズム
本報のバネモデルでは粘性抵抗を発現させるメカニズムを設けている。 Fig.2の赤枠部分
Fig.7は原子間に存在する引力と斥力の関係を表す力エネルギ場(通称、レナード・ジョーンズ・ポテンシャル)を表す。
右図は力エネルギ場を位置(原子間距離)で微分した力を表す。
原子間距離に応じて力の正側は斥力圏、負側は引力圏となる。
また、原子間距離に応じて斥力弾性域、引力弾性域、粘性域に分ける事が出来る。
弾性域と呼んだのは近似的にフックの法則が成り立つ=線形と見なせるという意味合いである。
一方、粘性域と呼んだ領域は非線形を示すが、このようなカーブを描くには原子間距離だけでなく、例えば二つの原子を引き離して行く際の時間(s)と距離(m)の関係=すなわち速度(ms-1)の要因が重なっている必要がある。
ここから速度(ms-1)に比例した力(N)を返す粘性抵抗係数Cm(Nsm-1)の存在が示唆される。 [4]
ここで、粘性抵抗係数は原子間距離がある程度大きくなる=ある変形量を超えないと発現しないと言える。
本報ではこの変形量を限界変形量と呼ぶ事にする。
実際の超伝導現象は絶対零度以上でも発現し、その温度は導体の元素に因って異なる事が知られている。
絶対零度を作り出す事は出来ないが、近傍まで温度を下げるには大きなエネルギが必要になるので、出来るだけ高い温度で超伝導が発現する元素の探索が行われている。
ここから、以下のメカニズムが考えられる。
・絶対零度近傍では物質が蓄える事が出来る熱エネルギEtは微少となり、伸縮の振幅は極めて小さい。
・従って限界変形量を超える事が出来ず、粘性抵抗係数が発現しない。
元素によって限界変形量が異なる件については、既研究ノート力学の双対性から見たプランク定数、及び物質破壊(崩壊)のモデル化 を参照されたい。
なお、後者では粘性抵抗係数Cmではなく塑性抵抗係数DHと呼んでいるがお互いに逆数の関係にあり、機能は同じである。
これは電磁気学のコンダクタンスG=1/電気抵抗係数Rの関係と同じである。
力学に於ける物質破壊(崩壊)とは物質の一端に巨大な速度を印加すると原子間距離が大きく引き離される=破断である。
電磁気学では、導体に巨大な電圧を印加すると焼損してしまう事に相当する。
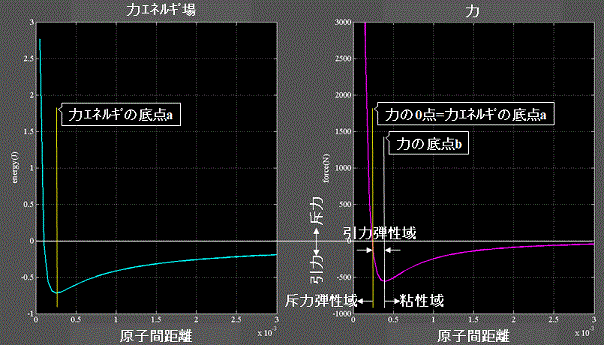
Fig.7 原子間に存在する引力と斥力の関係を表す力エネルギ場
|
本実験ではこのメカニズムを用いて、粘性抵抗の有無に因るバネの挙動の違いを観察した訳である。
一般的に、現実世界で働く機械は自動車のサスペンションのように、バネの振動を速やかに減衰させる為にダンパー機構=ショックアブソーバを組み合わせている。
これは設計的に意図して粘性抵抗を付与するものだが、電磁気学でこれに相当するのはコンデンサとコイルからなる共振回路を設計する場合、所望の電圧変化を得る為に様々な抵抗係数Rを持った素子が用意されている。
産業界ではダンパーや抵抗素子は製品として粘性抵抗係数Cmや抵抗係数R=1/コンダクタンスGで管理出来るので粘性抵抗や電気抵抗自体の発現メカニズムは工学の分野では不問にして来たと言える。
|
●マイズナー効果の解釈
超伝導現象が発現した導体の上に置いた磁石が斥力によって浮上するマイズナー効果が知られている。
補足資料に掲載した力学と電磁気学の相似則の表によると、力学の位置=変位=変形量は電磁気学の磁束と相似である。
ここから、超伝道現象発現時には導体に磁束が残留すると解釈出来る。
| バネ | 導体 |
速度印加を止めてもバネは伸縮し続ける
|
電圧印加を止めても電子は伸縮し続ける
|
単位区間は微少な質量と柔性の共振力学系である
|
単位区間は微少なコンデンサとコイルの共振回路系である
|
変位が残留し、変動し続ける
|
磁束が残留し、変動し続ける
|
|
●電気抵抗の物理的メカニズム
本報では力学と電磁気学の相似則を利用して超伝導現象が起きる仕組みを実体を伴うバネに置き換えて考察した。
一方、導体が持っている電気抵抗だが、例えば銅線とニクロム線(合金)の抵抗値は異なる。
元素の化学的な性質の違いは明らかになっているが、物理的なメカニズムは未解明である。
Cu、Ni、Crの原子の振る舞いの違いと推測出来るが、筆者は既研究ノート 力学の双対性から見たプランク定数、及び物質破壊(崩壊)のモデル化に於いて原子量と原子の限界変形量は反比例する事を示した。
その関係を用いると電気抵抗の物理的メカニズムは以下のように説明出来る。
・粘性抵抗発現のメカニズムの項で述べたように、粘性抵抗は限界変形量を超えると発現する。
・原子量が小さい元素は限界変形量が大きいので同じ速度印加に対して粘性抵抗が発現し難いと言える。
・原子量はCr<Ni<Cuの順であるからニクロム線の方が銅線より粘性抵抗が発現し難い。
・電気抵抗係数Rは粘性抵抗係数Cmの逆数であるから、ニクロム線の方が同じ電圧印加に対して電気抵抗が発現し易い。
・ここから逆に、同じ温度で電気抵抗が発現し難い=超伝導となり易い元素は原子量が大きい元素と予想される。
・あるいは、結合剛性の高い構造を持った合金や分子の探索が候補になると予測される。
送電という行為に限らず、現実界に起こる万物の事象はエネルギ保存則に従って時々刻々起こっている3つのエネルギの相互変換に帰すると言える。
| エネルギE = 速度エネルギEv + 力エネルギEf + 熱エネルギEt = const. |
(1.5) |
| エネルギE = 静電エネルギEC + 電磁エネルギEL + 熱エネルギEt = const. |
(1.6) |
化学反応も突き詰めれば異種元素間の電子の授受に帰するが、人体の中で起きている細胞増殖~代謝はアミノ酸やタンパク質の合成によって成り立っている。
しかしながら、時には製造不良と考えたくなるような不良タンパク質が合成されてしまう事がある。
起きて欲しくない疾病の中には癌=腫瘍の発現があるが、遺伝子が絡むものと製造不良に因るものが挙げられている。
製造不良は我々が日常利用する機械には付き物であり、継続的にゼロにすることはかなわない。
掛ける労力やコストを勘案して、ある確率で発生してしまう製造不良は許容していると言うべきであろう。
人体に起きて欲しくない事象に戻ると、それを発現させないためには電子の振る舞いを知る事が不可欠と考える。
エネルギは直接観測できない物理量である。
原子、電子が蓄えているエネルギをモデル上で可視化し、どのような状態にあるかを観察する事が望まれる。
|
もくじへ戻る
 まとめ
まとめ
| ・ |
柔らかい物質の物理機能モデルを用いて導体をバネに置き換える事で以下の知見を得た。
|
| ・ |
バネの一端に速度を印加する操作は、導体に電圧を印加する事に相当する。
|
| ・ |
バネの速度印加を止めると粘性抵抗によってバネの伸縮と移動は減衰して止まる。
|
| ・ |
バネの伸縮によって両端間に生まれる速度差は粘性抵抗によって熱エネルギに変換される。
|
| ・ |
その熱エネルギによってバネ自身の温度が上昇する。
|
| ・ |
これは導体に電圧を印加すると電気抵抗によって熱を持つ事に相当する。
|
| ・ |
絶対零度では粘性抵抗が発現せず、速度印加を止めるとバネの移動は止まるが、伸縮は続く。
|
| ・ |
これは導体内の電子の伸縮が残存し、電流が流れ続けると表現される事に相当する。
|
| ・ |
電子は完全剛体ではなく、伸縮する=すなわち大きさ~長さを持っていると見なす必要がある。
|
| ・ |
電気抵抗の物理的メカニズムを明らかにした。
|
| ・ |
超伝導が発現し易い材料として、原子量の大きな金属を含むか、結合剛性の高い構造を持った合金や分子の探索が候補になると予測される。
|
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年 P148
[2]:機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
[3]:次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年 P87
[4]:機械の力学 長松昭男 著 朝倉書店刊 2007年 P51
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年
・研究ノート 浮遊する柔らかい物質の振動解析 五十川晋一 著 2025年
・研究ノート 光速に関する考察 五十川晋一 著 2025年
・研究ノート 物質破壊(崩壊)のモデル化 五十川晋一 著 2025年
・研究ノート 力学の双対性から見たプランク定数 五十川晋一 著 2025年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート 電子レンジの物理モデル化
研究ノート パウリの排他原理のモデル化
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 




















