研究ノート
パウリの排他原理のモデル化
2025.8.1
五十川晋一
|
 目的
目的
質量を持つ物質に働く重力(万有引力)や電荷を持った物質に働くクーロン力は近接作用と呼ばれている。
万有引力の公式を以下に示す。
| F = Gg・(m1・m2) / L2 F:万有引力 m1、m2:物体の質量 L:2物体の重心間距離 Gg:万有引力定数 |
|
この式は力とその他の物理特性との関係を示しているが、力自体の発生メカニズムは不問にしている。
また、ニュートンが前提とする重心とは数学的に長さを持たない点であるのに対し、L:距離を分母に置いている点で矛盾が存在する。
この為、2物質間の距離がゼロでは重力は無限大になるという、数学的性質を抱えていると言える。
クーロン力の公式を以下に示す。
| F = 1 / 4πε0 ・(q1・q2) / L2 F:クーロン力 q1、q2:粒子の電荷 L:2粒子間距離 ε0:誘電率 |
|
この式は万有引力と同様に力とその他の物理特性との関係を示しているが、力自体の発生メカニズムは不問にしている。
万有引力の公式と異なるのは、q1、q2の正負号が同じ場合は斥力、異なる場合は引力となる。
パウリの排他原理とは、2つ以上の電子は、同一の状態を占めることはできない、とされている。
電子が2個存在する場合、両者は同じ電荷と質量を持つが、お互いに相手と反対の状態を持つと説明されている。
量子力学ではこの状態の違いを表現する為にスピンの向きという概念が用いられている。
電子同士は接触したり、合体する事が無く、電子間には引力が働くが、ある至近距離を境に斥力に転じると言われている。[1]
ここには両電子の状態がある距離を境に逆転する仕組みがあると考えられる。
筆者は先に物理機能モデル手法を用いて重力発現モデルを作成した。
本報ではクーロン力についても同じ考え方でモデル化し、二つの電子に重力、及びクーロン力を発現させることで接近、離反する状況の創出を試みる。
なお、物理機能モデル手法の詳細は補足資料に示した。
 もくじ
もくじ
●柔らかい物質について
●エネルギについて
・物質に蓄えられるエネルギ
・内包量と外延量について
・熱エネルギと力エネルギ、位置エネルギの等価性
・力学エネルギと熱エネルギの関係
●パウリの排他原理のモデル化
・スピンに代わる状態量
・伸縮による状態の遷移
・伸縮による粘性の発現
●机上実験
・実験用モデル
・パラメータ
・試験条件
・結果
●考察
・パウリの排他原理の役割
・力学と電磁気学の相似則
・電流の力学的解釈
・絶対零度について
●まとめ
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[2]
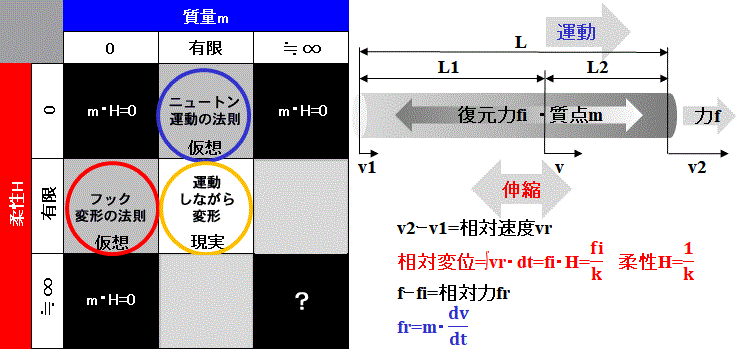
Fig.1
|
もくじへ戻る
 エネルギについて
エネルギについて
●物質に蓄えられるエネルギ
物質全般は絶対零度以上の温度にあるとき、熱エネルギを蓄え、かつ伸縮している。 *1
まず、伸縮している物質の力学的エネルギEは以下のように定義される。
| Ev = 1/2 m・v2 |
Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.1) |
| Ef = 1/2 H・f2 |
Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.2) |
| E = Ev + Ef = const. |
|
(1.3) |
上式は力学の双対性を現し、式(1.3)は対になったエネルギの和は常に一定となる事から、伸縮する物質に限ったエネルギ保存則と呼べる。補足資料1参照
次に、物質は絶対零度 0(k)=(-273.15℃)以上で熱エネルギEtは以下のように定義される。
| Et = m・Cp・T Et:熱エネルギ、m:質量、Cp:比熱、T:温度 |
(1.4) |
*1:ド・ブロイの物質波と呼ばれ、物質全般はバネと見なす事が出来る。
|
●内包量と外延量について
●熱エネルギと力エネルギ、位置エネルギの等価性
●力学エネルギと熱エネルギの関係
補足資料2に示すように、Et = Ef = 1/2 H・f2 と置けば力fが求められる。
この力fを最初にバネに印加しておくことで、物質が熱エネルギEtを蓄えている事を力学的にバネの伸縮に置き換えて表現する事が出来る。
これは式(1.4)が示された時、質量mを持つ物質とは変形しない完全剛体をイメージするかもしれないが、バネのように柔性Hを併せ持って伸縮するという見方をすると言う事である。
又、この力fは地球上でバネの上端を固定して垂直に吊るして静止している時にバネ内部に生ずる復元力と等価であり、重心に作用する重力と釣り合っている、すなわち万有引力と等価と言える。 *2
バネを吊るした状態から解放すれば落下を始めるがその時、式(1.3)に従って力エネルギEf=位置エネルギは逐次速度(運動)エネルギEvに変換され、両者の和は常に一定を保つ。
次に、絶対零度下ではバネの熱エネルギEt = 0、バネ内部の復元力f = 0になるので力エネルギEf = 0となる。
従って何もしなければバネは伸縮しないが、水ヨーヨーを振るように速度を印加すれば伸縮し始める。
この時、物質が蓄える力学エネルギEは外延量と内包量の和となる。
エネルギEとは本来、外延量 + 内包量の形であり、熱エネルギEtだけは内包量単独という位置づけと言える。
これらを整理したのが以下の表1である。
| 力学エネルギE |
| 速疎(運動)エネルギEv | |
| 力(位置)エネルギEf | 熱エネルギEt |
|
|
|
|
| 電気エネルギE |
|
|
|
|
*2:ニュートンが万有引力の法則を示した時、フックは同じ概念は自分が先に考えたと反論しており、ニュートンが復元力という見方をしていない点を指摘したものと思われる。
これを機に両者は反目するようになった。
フックの死後、ニュートンは彼の文書や実験装置を焼却しており、フックの復元力の見方は約2世紀後にアインシュタインが一般相対性理論に於いて空間の歪みという概念を用いるまで、顧みられる事は無かった。
なお、アインシュタインは力学的なアプローチではなく、数学の力を借りて空間の歪みを表現している。
|
もくじへ戻る
 パウリの排他原理のモデル化
パウリの排他原理のモデル化
●スピンに代わる状態量
量子力学では電子同士はお互いに異なる状態を取る事を表現する為にスピンなる概念が用いられている。
電子のスピンの状態を表す量として角運動量なる物理量が使われている。
一方、物理機能モデルでは物質を質量mと柔性Hを対にして扱うので自転しながら運動する物質ではなく、バネのように伸縮しながら運動する物質が表現されている。
伸縮は波動であり、物質を粒子と波動の両面で表現している事になる。
本報では物理機能モデルの基本モデルをそのまま電子のモデルとしている。
電子の質量mは9.1093837015×10−31 kgとされているが、柔性Hは測られていない。
柔性Hを定義する為には電子の変位=長さと復元力が判っていなければならないが、不確定性原理により観測が困難という事情がある。Fig.2参照
本報では伸縮する物質がモデル化出来れば良いので、質量mと柔性Hを仮想の値としている。
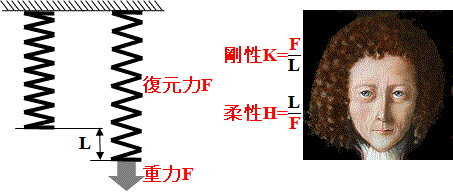
Fig.2
|
|
●伸縮による状態の遷移
パウリの排他原理と呼ばれるようになる以前、パウリは二つの状態を取るという事を二価性と呼んでいた。
伸縮している物質は数学的にも正弦波のように状態が規則正しく変化する。
二つの電子に斥力が働く場合と引力が働く場合を作り出す為に以下のような仮説を立てた。Fig.3参照
・状態1:両電子がお互いに縮み方向の場合、クーロン力は引力となる。
・状態2:両電子がお互いに伸び方向の場合、クーロン力は斥力となる。
モデル化に際し、この仕組みを組み込む。(Fig.5のモデル図の中の大きい赤枠部分)
両電子の隣接距離がある閾値以下となる事をトリガーに状態1と2が半周期毎に交互に発現する。
引力に因り接近する両電子は途中で離反し、斥力が無くなると再接近する。
これが繰り返されると、両電子は付かず離れず、ある閾値=隣接距離を保ちながら浮遊する状態となる。
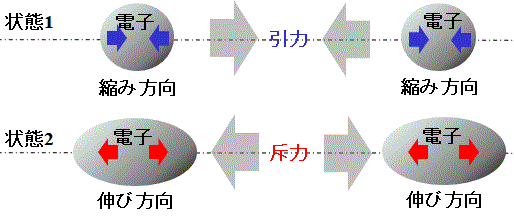
Fig.3
|
|
●伸縮による粘性の発現
|
筆者は以下の事例から電子の振る舞いには斥力だけでなく、粘性なる物理量が発現する仕組みがあると考えた。
・気体分子(O2、N2、H2O、CO2等)が存在する空間中を帯電した物質が移動する際に、速度に比例した抵抗力を受ける。
・物質に帯電した電荷を取り除くと抵抗力が減じる。
・例として、自動車の車体や各装置に帯電した静電気をアースして逃がすと、走行抵抗や各装置に働いている抵抗が低減する事が経験的に知られている。
・また、地球表面で太陽光により大気が温められて上昇気流が生まれ、大気の分子間の摩擦による帯電で雷雲が生じると説明されている。
・しかしながら相手が静電気なので観測が難しく、これらのメカニズムは未解明である。
こうした現象から、原子の集合体である物質が気体分子で満たされた空間中を移動する際に、原子と気体分子が抱える電子同士が近接する際に、ある振る舞いをする仕組みを考えた。
Fig.4は原子間に存在する引力と斥力の関係を表す力エネルギ場(通称、レナード・ジョーンズ・ポテンシャル)を表す。
右図は力エネルギ場を位置(原子間距離)で微分した力を表す。
原子間距離に応じて力の正側は斥力圏、負側は引力圏となる。
また、原子間距離に応じて斥力弾性域、引力弾性域、粘性域に分ける事が出来る。
弾性域と呼んだのは近似的にフックの法則が成り立つ=線形と見なせるという意味合いである。
一方、粘性域と呼んだ領域は非線形を示すが、このようなカーブを描くには原子間距離だけでなく、例えば二つの原子を引き離して行く際の時間(s)と距離(m)の関係=すなわち速度(ms-1)の要因が重なっている必要がある。
ここから速度(ms-1)に比例した力(N)を返す粘性抵抗係数Cm(Nsm-1)の存在が示唆される。 [3]
本報では上記の考え方から、原子間に存在する引力と斥力の関係は電子間にも適応出来るという仮説を立てた。
これは前述の二つの電子に斥力が発現する閾値=隣接距離から離れて行く際に粘性が発現するというものである。
モデル化に際し、合わせてこの仕組みも組み込んだ。(Fig.5のモデル図の中の小さい赤枠部分)
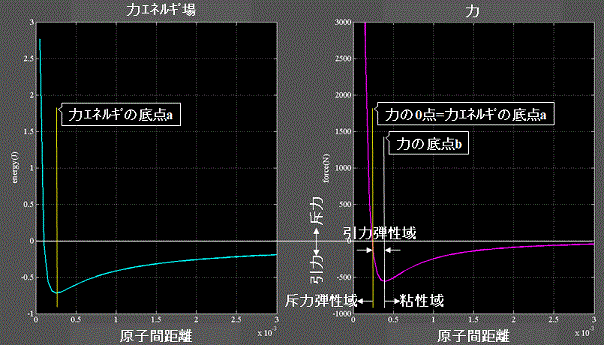
Fig.4 原子間に存在する引力と斥力の関係を表す力エネルギ場
|
|
もくじへ戻る
 机上実験
机上実験
●実験用モデル
Fig.5は二つの物質モデルの間に空間に相当するモデルを配置したものである。
空間モデルは両端の物質モデルと同じであり、見かけ上3連モデルの構成である。
但し、両物質モデルと空間モデルは相互に結線されておらず、空間モデルから出力された力のみ両物質モデルに印加する回路構成になっている。
空間モデル内に両脇の物質の質量、柔性、長さ、隣接距離の情報を使って重力・クーロン力を発現させる機構モデルを組み込む。(大きい赤枠)
なお、補足資料で示した基本モデルは物質の一端が固定の場合のみ適応出来るが、一端に速度を印加したり解放して宙を浮遊する場合は基本モデルの2連以上でなければならない。
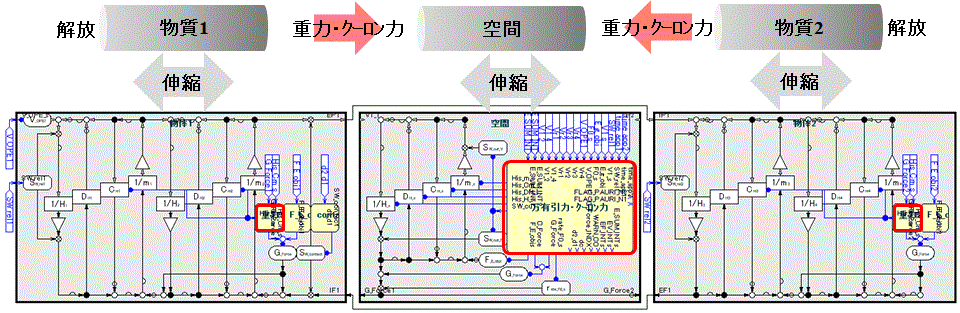
Fig.5
|
|
●パラメータ
・仮想電子質量m:1.0(kg)
・仮想電子柔性H:1.0e−5(mN−1)(剛性kの逆数)
・仮想電子長さL:0.1(m)
・仮想電子外径Φ:1.0(m)
・仮想電子比熱Cp:435(JKg-1k-1)(鉄の値を流用)
・温度:273.1(k)= 0(℃)、及び絶対零度 = 0(k)= -273.15(℃)の2水準
・重力:0=無重力下とする
|
●試験条件
・サンプリング時間:10-5(s)
・両電子の隣接距離L:0.5(m)
・両電子に式(1.4)に因って決まる熱エネルギEtと等価な力fを印加する。印加方法は補足資料9参照
・印加完了と同時に解放する。
・この操作は無重力空間で2個のバネを向かい合わせ、引っ張ってから解放する操作に相当する
・結果説明の為に試験中の状態を以下の3caseに分ける。
case1:解放後の浮遊状態
case2:電子1に右向き速度を一定時間、印加する=右向きに押す
case3:case2を絶対零度で行う
 Fig.6
Fig.6
|
|
●結果
|
Fig.7_1~10に各物理量の時系列波形を示す。
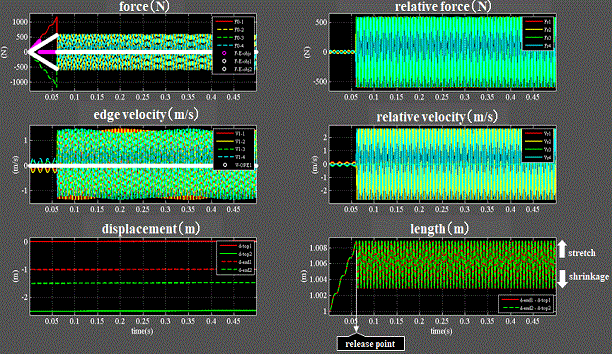
Fig.7_1 case1(浮遊状態)
・左上段:初期熱エネルギEtを力fで印加すると(白プロット)両電子は伸縮を始める。
・力(復元力)はお互いに逆位相で変動する。
・左中段:速度も同様に逆位相で変動する。
・左下段:変位も同様に逆位相で変動する。
・右下段:両電子の長さは同位相で伸縮している。(上方向が伸び側、下方向が縮み側)
|
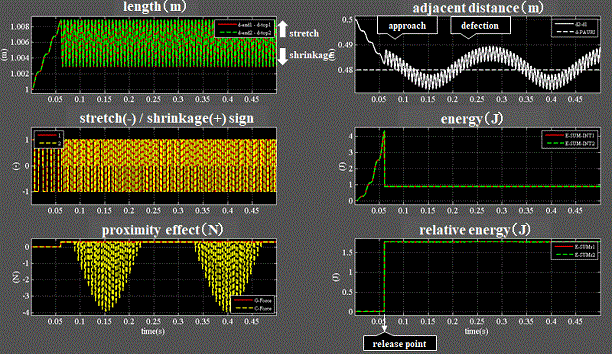
Fig.7_2 case1(浮遊状態)
・左上段:電子1(赤)、電子2(緑)の長さは同位相で伸縮している。
・左中段:縮み側(+1)/伸び側(-1)を表す符号
・左下段:伸び側の時のみクーロン力(黄)は斥力(負)に切り替わる。 赤は重力=引力(正)である。
・右上段:両電子の隣接距離。接近していた両電子は斥力を受けると途中で離反し、斥力が無くなると再接近する。
・これが繰り返され、両電子はある隣接距離の幅を保って浮遊する状態となる。
・右中段:両電子のエネルギ(外部座標から観測)は電子自身の速度変動に因って変動しながら安定した状態を保つ。
・右下段:両電子の相対エネルギ(電子自身の座標から観測)も安定した状態を保つ。
|
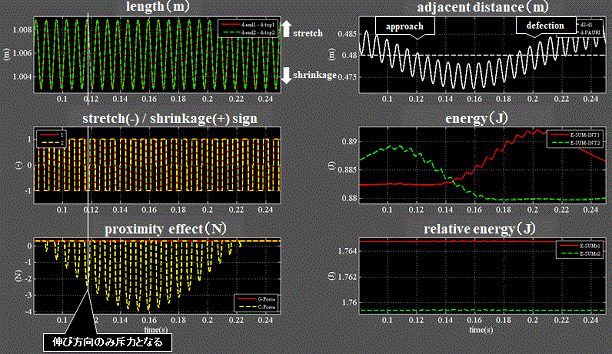
Fig.7_3 case1(浮遊状態) ズーム
・左上段:電子1(赤)、電子2(緑)の長さは同位相で伸縮している。
・左中段:縮み側(+1)/伸び側(-1)を表す符号
・左下段:クーロン力(黄)は縮み側では引力(正)、伸び側では斥力(負)に切り替わる。
・重力(赤)は常に引力(正)だが、クーロン力(黄)は引力と斥力が交互に発現する。
|
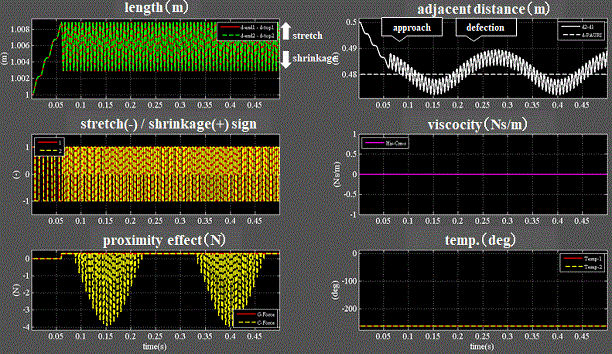
Fig.7_4 case1(浮遊状態)
・右中段:粘性抵抗=0である。
・右下段:温度は変化無し。
|
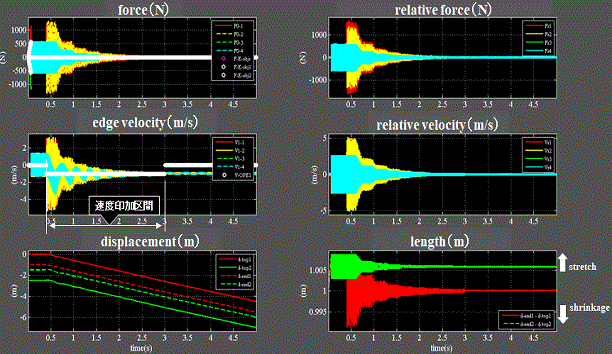
Fig.7_5 case2(速度印加)
・左中段:電子1の左端に時刻0.4~3.0秒の区間で-1(m/s)の速度(縮める方向)を印加する。(白プロット)
・左上段:粘性抵抗が発現し、力(復元力)は減衰して行く。
・左下段:変位、電子1(赤)は電子2(緑)に接近するが、斥力を受けて電子2は離れようとする。
・右下段:長さ、電子1(赤)と2(緑)で異なる。速度を印加した電子1の方が伸縮量が大きい。
・速度印加を止めると伸縮量は減衰してゆく。
|
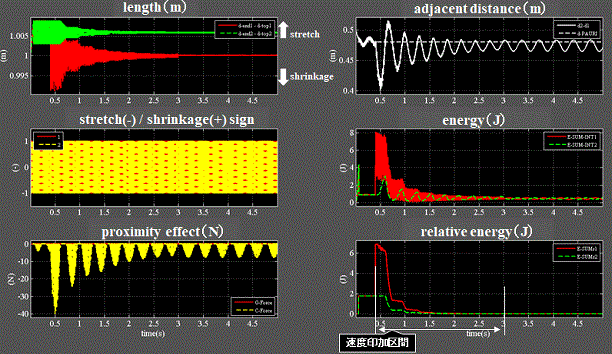
Fig.7_6 case2(速度印加)
・左上段:長さは電子1(赤)と2(緑)で異なる。速度を印加した電子1の方が伸縮量が大きい。
・速度印加を止めると伸縮量は減衰してゆく。
・右上段:隣接距離は速度印加の影響はあるがほぼ一定を保つ。
・右中段:両電子のエネルギ(外部座標から観測)は電子自身の速度変動に因って変動しながら減衰してゆく。
・右下段:両電子の相対エネルギ(電子自身の座標から観測)も減衰してゆく。
|
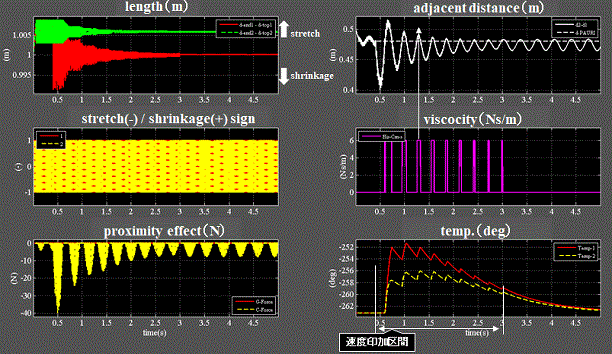
Fig.7_7 case2(速度印加)
・右中段:両電子が離反するタイミングで粘性抵抗が発現する。
・右下段:速度印加によるエネルギの一部は粘性抵抗に因って熱エネルギに変換され、両電子の温度が上昇する。
・速度印加を止めると温度は降下してゆく。
|
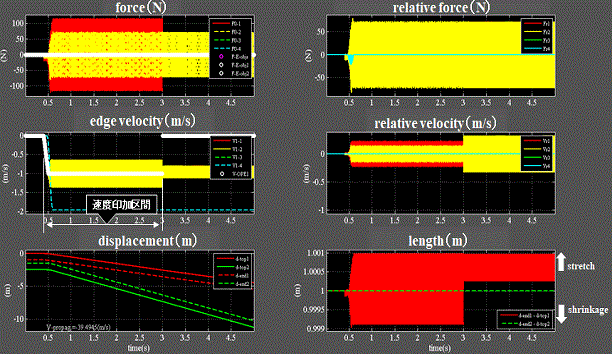
Fig.7_8 case3(速度印加+絶対零度)
・左中段:電子1の左端に時刻0.4~3.0秒の区間で-1(m/s)の速度を印加する。(白プロット)
・電子2は斥力を受けて同方向に速度を持つ(水色)。
・速度印加を止めても電子1は慣性によってその速度を維持する(黄)。
・左上段:速度印加を止めても電子1はその力(復元力)の変動を維持する。(黄)
・左下段:電子1(赤)は負方向に移動を続け、電子2(緑)は斥力による速度変化を維持して移動を続ける。
・右下段:長さは電子1(赤)は速度印加によって伸縮を始めるが、電子2(緑)は伸縮せず一定を保つ。
・粘性抵抗が発現しないので速度印加を止めても電子1(赤)は伸縮を続ける。
|
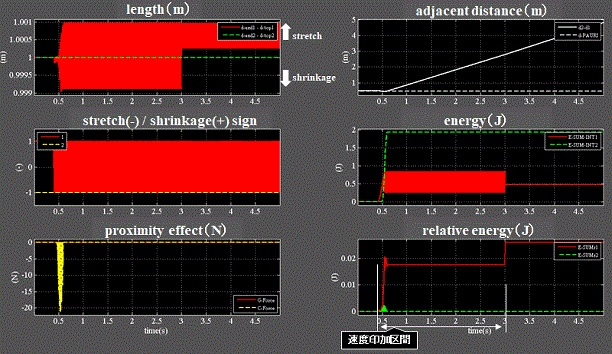
Fig.7_9 case3(速度印加+絶対零度)
・左下段:クーロン力(黄)が斥力(負)に切り替わるのは最初の一回のみである。
・右上段:接近していた両電子は途中で離反し、その後両電子は離れ続ける。
・これは最初の斥力に因って電子2は電子1に弾かれた格好となる。
・右中段:電子1(赤)のエネルギ(外部から観測)は速度印加中は伸縮によって変動する。
・一方、電子2(緑)は最初の斥力によるエネルギを受けて一定を保つ。
・右下段:電子1(赤)の相対エネルギ(電子自身の座標から観測)は速度印加を受けている間は一定を保つ。
・印加を止めると解放された状態の値を保つ。
・電子2(緑)は最初の斥力を受けてエネルギは増加するが、斥力が無くなるとゼロに戻る。
|
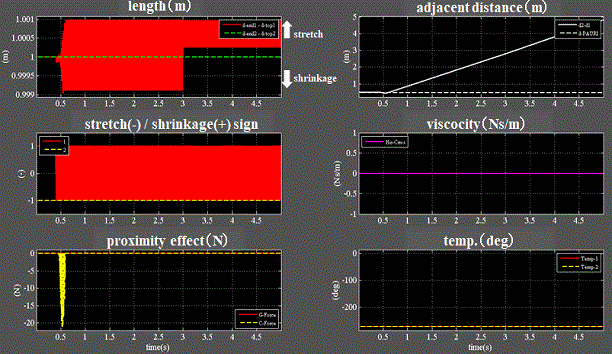
Fig.7_10 case3(速度印加+絶対零度)
・右中段:粘性抵抗は発現しない=0である。
・右下段:温度は変化無し。
|
以下に結果を要約する。
| case1 |
・二つの電子は付かず離れず、ある閾値=隣接距離を保って伸縮しながら浮遊する。 |
|
case2
|
・一方の電子に速度を印加して相手の方向に押すと相手は隣接距離を保とうとして離れる。
・離れる際に粘性抵抗が発現する
・速度印加を止めると両電子の伸縮は減衰する。
|
|
case3
|
・絶対零度下では二つの電子は伸縮しない。
・一方の電子に速度を印加すると伸縮を始めるが、相手は伸縮しないので粘性抵抗が発現しない。
・速度印加を止めても伸縮し続ける。
|
|
もくじへ戻る
 考察
考察
●パウリの排他原理の役割
・case1、2についての考察:
二つの電子が存在すれば重力・クーロン力=近接作用が働くが、両者は接触しない。
この結果からパウリの排他原理には、お互いに伸縮しながら隣接距離を保つ働きがあると推察される。
このような仕組みは、二人の人間がお互いにソーシャルディスタンス(縄張り)を保とうとする様に似ている。
また、毛細血管や樹木の先端は血管や枝同士が重ならないように成長=細胞分裂を止める自律機能があると考えられる。
これはシステムの中のリミッター機能と言える。
血管や枝を構成する原子に付帯する電子同士が近接状態を感知するセンサーの役割を果たしていると考えられる。
人体の毛細血管の総延長は10万Kmを超えると言われており、生命を維持する為に効率よくエネルギを運ぶ驚異的なシステムと言える。
このような、お互いが重ならないという仕組みは数学的にはフラクタルなる性質と言われている。補足資料5参照
フラクタルとは部分の仕組みが全体の仕組みと相似になっている性質であり、毛細血管が重ならない仕組みと人間が社会の中でソーシャルディスタンスを保とうとする仕組みは同じと言えるかもしれない。
もし、このリミッター機能が正常に働かなかった場合は細胞分裂が止まらず、細胞同士が干渉してしまい、腫瘍とはこうして発現するのかもしれない。
動物の細胞分裂は細胞を縛って分割させるための紐の役目をするアクチンと呼ばれるタンパク質が存在する。 [4]
本報の机上実験から、タンパク質を構成する原子に付帯する電子が紐を縛るか否かというスイッチ機構となっている可能性が示唆される。
・case3についての考察:
絶対零度以上と絶対零度では前述のように、電子(バネ)が伸縮するか否かという違いがある。
この過程は一方の電子に速度を印加して相手の方向に押す事になるが、Fig.7_9に示したように、斥力が発生するのは1回だけである。
この為に隣接距離を保って浮遊する事が出来ず、同一方向に移動しつつ、お互いに離れてゆく。
また、粘性の発現機構を組み込んでいるが、速度を印加しない電子の方は伸縮しないので、両電子間には粘性が発現せず、両電子の動きは減衰する事が無い。
こうした様相から、リミッター機能やセンサー機能、粘性発現機構とは伸縮があって初めて動作すると言える。
センサーとは原理的に、観測する速度や力という物理量の変動があって初めて動作するものである。
従って、本報の机上実験から、伸縮する状態=絶対零度以上がパウリの排他原理が働く必要条件と言う事になる。
|
●力学と電磁気学の相似則
補足資料に掲載した力学と電磁気学の相似則の表に従い、本報の電子(バネ)モデルによる机上実験に於いて得られた知見は、電磁気学の導体に置き換える事が出来る。表2参照
電磁気学上の導体とは、例えば銅原子の連鎖と見れば力学上のn連バネと相似である。
絶対零度近傍では電圧印加を止めても電流が残る(流れ続ける)、超伝導現象が知られている。
この詳細は既研究ノート 力学の双対性から見た超伝導現象を参照されたい。
| 表2 |
電子(バネ) |
導体(n連バネ) |
|
絶対零度以上
|
速度を印加する
↓
粘性抵抗によって熱エネルギに変換される。
↓
電子の温度が上昇
↓
速度印加停止
↓
粘性抵抗によって電子の速度、復元力は減衰する
|
電圧を印加する
↓
電気抵抗によって熱エネルギに変換される
↓
導体の温度が上昇
↓
電圧印加停止
↓
電気抵抗によって導体の電圧、電流は減衰する
|
|
絶対零度
|
電子は伸縮しないので粘性抵抗が発現しない
↓
速度印加を止めても電子の復元力が残る
|
電子は伸縮しないので電気抵抗が発現しない
↓
電圧印加を止めても電流が残る(流れ続ける)
|
|
●電流の力学的解釈
本報のモデルは電子単体だが、導体が純銅製であれば銅原子の連鎖と言える。
導体中の銅原子に付帯する最外殻電子=自由電子が本報の電子単体モデルに相当する。
補足資料に掲載した力学と電磁気学の相似則の表によれば、
・力学上の速度vと電磁気学上の電圧Vは相似である。
・力学上の力fと電磁気学上の電流Iは相似である。
ここから、導体中を電流が流れるという現象は以下のように解釈出来る。 Fig.7参照
・導体の端から端まで自由電子が移動するのではない。
・導体の一端の電子が速度印加を受ける=電圧を印加されて押されると隣の電子は斥力によって離れようとする。
・n個の原子が連なる導体では電子から電子に斥力が伝播して行く。[5]

Fig.7
|
|
●絶対零度について
机上実験のcase3では絶対零度を条件としている。
本報はパウリの排他原理のモデル化をテーマに始めたが、パウリが当初に考えた二価性には例外があり、それが絶対零度なる条件と言う事になる。
絶対零度とは理論上の熱エネルギEt=0の状態であるが、物質が伸縮出来ない状態と言える。
従って、伸び過程と縮み過程という二つの状態は存在し得ない。
あるいは、絶対零度下では電子のスピンが止まるという解釈も出来るであろう。
一方、現実に存在する宇宙は絶対零度では無く、温度を持つとされている。*4
これはド・ブロイの物質波が発現し、物質は伸縮出来る状態にあると言える。
補足資料に示すように、物理機能モデル手法は物質を質量mと柔性Hを対にする事でバネと見なしている。
ここでcase3、及び補足資料9で示したように、以下のいずれかの操作が呼び水となって伸縮を始める事が出来る。
・電子=バネの一端に速度v=外延量を印加する。
・熱エネルギEtに相当する力f=内包量を印加する。
ここから宇宙の起源と考えるビッグ・バンとは、伸縮出来ない状態から脱出する呼び水に喩えられるかもしれない。
*4:3(k) = -270(℃)とされている。
|
もくじへ戻る
 まとめ
まとめ
| ・ |
物理機能モデル手法による二つの電子とそれに挟まれる空間のモデル化、及びパウリの排他原理のモデル化により以下の知見が得られた。
|
| ・ |
二つの近接する電子間に重力とクーロン力を発現させる事ができた。
|
| ・ |
二つの電子を近接させると、付かず離れず、ある閾値=隣接距離を保ちながら浮遊する状態が創出できた。
|
| ・ |
電子の一方に速度を印加して相手の方向に押すと相手は隣接距離を保とうとして離れる。
|
| ・ |
パウリの排他原理には、お互いに伸縮しながら隣接距離を保つ働きがあると推察される。
|
| ・ |
絶対零度以上では速度印加を止めると電子の伸縮は止まる。
|
| ・ |
絶対零度下では速度印加を止めても電子は伸縮し続ける。(電流が流れ続ける)
|
| ・ |
これらの知見から導体を電流が流れる仕組みを力学的に説明できた。
|
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年 P86
[2]:機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
[3]:機械の力学 長松昭男 著 朝倉書店刊 2007年 P51
[4]:タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年 P136
[5]:次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年 P87
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・タンパク質の音楽 深川洋一 著 ちくまプリマーブックス 1999年
・つくばサイエンスニュース パウリの排他原理による斥力(せきりょく)の起源を実験で検証 2022年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート 電子レンジの物理モデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 
























