研究ノート
電子レンジの物理モデル化
2025.8.14
五十川晋一
|
 目的
目的
電子レンジが電磁波を食品に照射すると加熱されるメカニズムは以下のように説明されている。
・電磁波は電界と磁界が周期的に変動する空間の歪みの伝播である。
・空間の歪みが食品に含まれる水分子を加振させる事で温度が上昇する=加熱される。
しかしながら、物質が加振されて温度が上昇するメカニズムは明らかになっていない。
本報ではこの現象を物理機能モデル手法で模擬し、力学的なメカニズムを考察する。
なお、物理機能モデル手法の詳細は補足資料に示した。
 もくじ
もくじ
●柔らかい物質について
●電子レンジモデル化の考え方
●机上実験
・電子レンジの物理機能モデル
・パラメータ
・試験条件
・結果
●考察
・物質の励起について
・空間の考え方
・電場と重力場について
・磁場とバネ場について
・重力波について
・速度=外延量と力=内包量について
・速度変化を印加するタイミングについて
・タイミングと量子もつれについて
●まとめ
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[1]
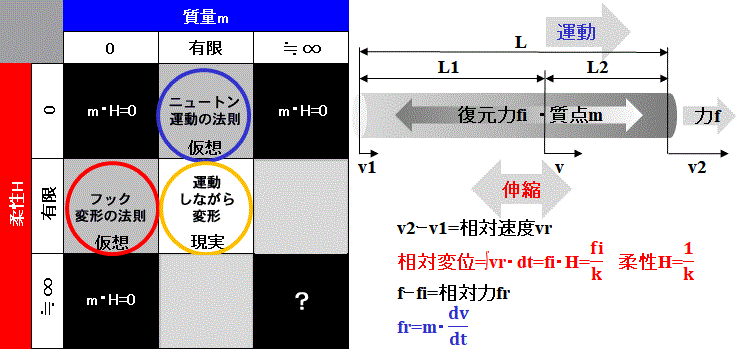
Fig.1
|
もくじへ戻る
 電子レンジモデル化の考え方
電子レンジモデル化の考え方
|
Fig.2_1に電子レンジの概念図を示す。
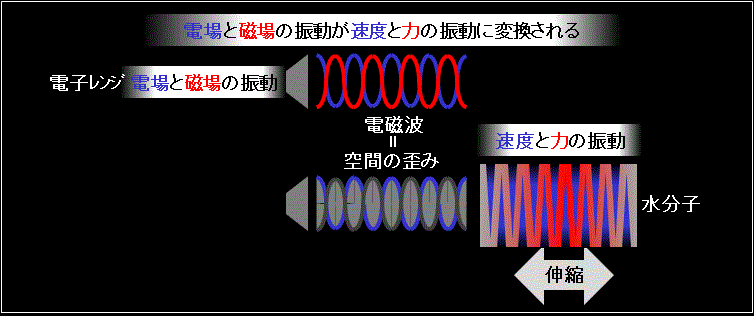
Fig.2_1
・電子レンジは電磁波を発生させるが、電磁波は電場と磁場の振動による空間の歪みの伝播である。
・空間の歪みは水分子を加振し、分子が蓄えるエネルギを増加させる。
・エネルギの増加分が温度の上昇となって現れる。
・すなわち、空間は実体が無くてもエネルギを伝播する機能を持っていると言える。
|
Fig.2_2に電子レンジのモデル化の概念図を示す。
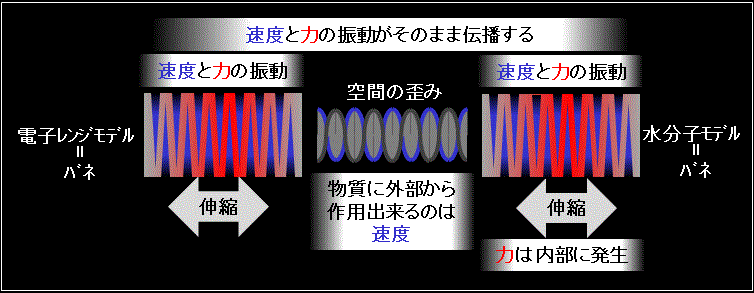
Fig.2_2
・電子レンジ、及び、水分子を実体の有るバネに置き換える。
|
次に力学の双対性を踏まえてモデル化の考え方を示す。
電磁波のエネルギ、及び伸縮するバネに蓄えられているエネルギは以下の通りである。
| EC = 1/2 C・V2 |
EC:電場の静電エネルギ、C:コンデンサ容量、V:電位差 |
(1.1) |
| EL = 1/2 L・I2 |
EL:磁場の電磁エネルギ、L:コイルのインダクタンス、I:電流 |
(1.2) |
| E = EC + EL = const. |
|
(1.3) |
| Ev = 1/2 m・v2 |
Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.4) |
| Ef = 1/2 H・f2 |
Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.5) |
| E = Ev + Ef = const. |
|
(1.6) |
上式のように式の形は同一であり、実体の無い電磁波の電場と磁場の振動は、実体のあるバネの伸縮による速度と力の振動と力学的に相似である。補足資料●力学と電磁気学の相似則参照
そこで、Fig.2_2のように電子レンジの電磁波発生回路(L・C回路)を実体のあるバネに置き換え、片側を固定して加振させるとバネ解放端は速度変化を生じ、伸縮を始める。
この速度変化はバネ解放端に隣接する空間に伝播し、空間の歪み=伸縮が生じる。
同様に水分子を実体のあるバネに置き換えると、空間に隣接する端部は空間の伸縮による速度変化を受けて力=復元力が発生し、伸縮を始める。
これは実体の無い空間を媒介にして片方のバネが他方のバネを励起させると表現出来る。 励起については別途考察する。
水分子側バネは電子レンジ側バネからパワ(Js-1)=端部の速度(ms-1)×内部の復元力(N)を印加された事になる。
パワは単位時間当たりのエネルギであり、瞬時エネルギと呼ぶ事も出来る。
パワ(Js-1)×電磁波照射時間(s)はエネルギとなり、これによって水分子側バネの温度が決まる。
次に、電子レンジ側バネの加振方法を以下に示す。
電子レンジが対象物質に与える熱エネルギEr(wh)は、
ワット数=P(w)と照射時間t(h)と置くと、
| Er = P・t(wh) 1(wh)=3600(J) |
(1.7) |
この熱エネルギErをバネの振動エネルギに置き換える。
熱エネルギErは同じ内包量である力エネルギEfに変換出来るので、Er = Ef = 1/2 H・f2 の関係から力fが求められる。
この力fを電子レンジ側バネに印加するとバネは伸縮を初め、その端部の速度変化が電磁波による周期的な電場=空間の歪みに相当する。
内包量については補足資料3参照
次に、水分子側バネについてその温度に相当する熱エネルギEtを振動エネルギに置き換える。
物質は以下の式で決まる熱エネルギEt(J)を蓄えて振動している。
これは量子力学的な視点から出発したド・ブロイの物質波の考え方である。
| Et = m・Cp・T Et:熱エネルギ、m:質量、Cp:比熱、T:温度 |
(1.8) |
電子レンジ側バネを伸縮させるのと同様に、Et = Ef = 1/2 H・f2 の関係から力fが求められる。
この力fを最初に水分子側のバネに印加しておく事で、熱エネルギを蓄えている事を力学的にバネの伸縮に置き換えて表現する事が出来る。
印加方法については補足資料9参照
|
もくじへ戻る
 机上実験
机上実験
●電子レンジの物理機能モデル
Fig.3にモデル図を示す。
基本モデルを用いて電子レンジと水分子を対にする。
両モデルは基本モデルを2連にしたものである。
但し、両モデルは結線されておらず、電子レンジモデル側バネ端部速度のみが水分子側バネの速度端子に入力される。
ここで電磁波が実体の無い空間を伝播するのは判るが、実体のあるバネが物理的に結線されていないのに、どうやって速度を伝える事ができるのか?という疑問が生じる。
これについては別途考察する。


Fig.3
|
|
●パラメータ
・質量m(電子レンジ側):0.015(kg)×2 (L・C回路のコンデンサの静電容量Cに相当する)
・柔性H(電子レンジ側):1.0e−5(mN−1) (L・C回路のコイルのインダクタンスLに相当する)
・質量m(水分子側):0.005(kg)×2
・柔性H(水分子側):1.0e−5(mN−1)
・比熱Cp(水):4217(JKg-1k-1)
・初期温度(水分子):278.15(k) = 5(℃)
・環境温度:278.15(k) = 5(℃)
・加熱パワ:0.04217(Js-1)
・電磁波照射時間:0.02(s)
・加熱エネルギ:0.04217×0.02 = 0.008434(J)
|
●試験条件
・サンプリング時間:10-5(s)
・水分子に初期熱エネルギ印加後、時刻0.03~0.05秒の間、加熱エネルギ(電磁波相当)を印加する。
・なお、水分子は熱伝達の無い断熱条件下とする。
|
●結果
|
Fig.4に各物理量の時系列波形を示す。
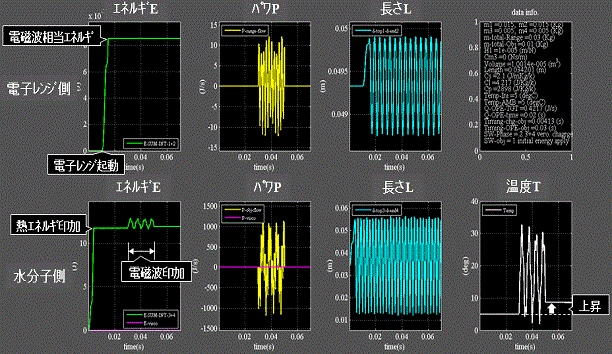
Fig.4
・上段は電子レンジ側、下段は水分子側を示す。
・1列目:バネに蓄積されているエネルギ。
・2列目:バネ端のパワ。
・3列目:バネ全長。
・1列目下段:水分子に初期温度に於ける熱エネルギを印加すると伸縮を始める。
・4列目:水分子側温度 時刻0.03秒で電磁波相当のエネルギを印加すると水分子は加振されて上昇する。
|
Fig.5に水分子側バネについて、X軸:端部速度v、Y軸:復元力Fに取ったリサージュ波形を示す。
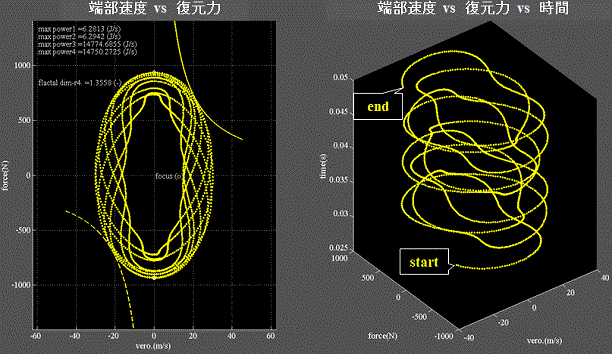
Fig.5
|
|
もくじへ戻る
 考察
考察
●物質の励起について
本報では二つのバネを物理機能モデルによって表現し、電子レンジに相当する側のバネを伸縮させ、その端部の速度変化を水分子に相当するバネ端部に印加している。
補足資料3に示すように、力学的に物質を操作出来るのは速度=外延量だけであり、力=内包量は物質内部に生じる。
これについては後段で検証した事例を示す。
水分子側のバネ端部に速度を印加するという操作は、例えば水ヨーヨーを振る事に相当する。 Fig.6参照
その隣は同様に縁日で良く見かける柔らかいバネである。
このバネの元祖はSLINKYと呼ばれ、米国で1945年に玩具として登場し、その亜流が世界中に流布している。
水ヨーヨーやバネを振る際、一端に速度変化を与えているように、電子レンジ側のバネの振動周期を持った速度変化を水分子に印加する事になる。
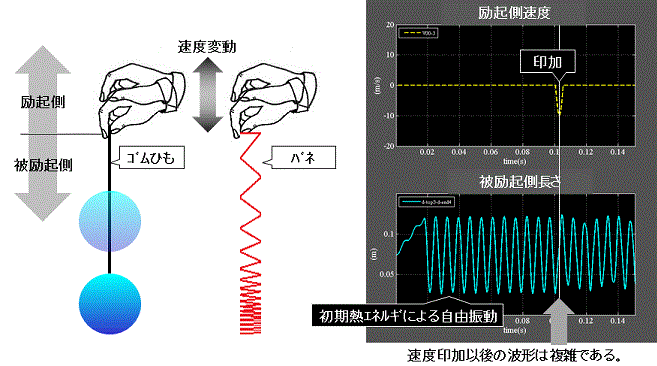
Fig.6
|
ここで印加しているのは速度変化だが、これを受けて水分子側バネ内部には復元力が生じ、実際には水分子には
パワP(Js-1) =速度 ×復元力 が印加された事になる。
これはパワとは復元力が生じて初めて印加されるという事であり、力学本来の作用~反作用の原理と言える。*1
ここから励起とは物質にエネルギを印加する事で、蓄えているエネルギ、及び振動モードが変わる現象と言える。
電子レンジの力学的メカニズムは水分子の励起と言える。
そして水分子の温度の上昇は印加されたパワに因るものと言える。
次に、印加しているのは速度変化なので、水分子は式(1.4)の速度(運動)エネルギを蓄えると考えがちである。
しかし、柔性Hによって生じる復元力によって式(1.5)の力(変形)エネルギも蓄えている事になるのである。
仮に水分子を柔性H=0=完全剛体としてしまうと復元力を返す事が出来ないので力(変形)エネルギは蓄える事が出来ず、式(1.6)は成り立たなくなってしまうのである。
つまり、質量mを持つ物資は同時に柔性Hを持つ=質量mと柔性Hは切り分ける事が出来ないのである。
また、復元力が返らなければ速度が印加されてもパワはゼロ=エネルギが印加出来ないのである。
速度を加えても復元力が返ってこない状態が、のれんに腕押し=パワが掛けられなかった状態である。
これが力学の双対性であり、これを数学的に示したのが補足資料1である。
本報ではパラメータとして電子レンジ側バネ質量を水分子側バネ質量の3倍にしており、(柔性Hは同一としている)水分子側は自身の固有周期と異なる周期の速度変化を印加されるので、複雑な振動モードで励起される事になる。
更に、Fig.2のモデル図に示すように電子レンジ側、水分子側の両バネは質量mと柔性Hの対を2連にしているので、モデルは非線形となり、Fig.5に示したような複雑なモードを持っている。
これはオモリを2連にした二重振り子のオモリの軌跡と同様の振る舞いをし、カオス軌道と呼ばれている。補足資料4参照
仮に電子レンジ側、水分子側のバネの質量を同じにする=固有振動数を合わせれば共振する事になる。
この原理はレーザー医療に応用されており、Fig.9にその例を示す。
実際の電子レンジから発生する電磁波の振動数は規格で2.4ギガ(109)Hzと決められており、水分子の固有振動数はおよそ1012~1015Hzなので共振を避けていると言える。
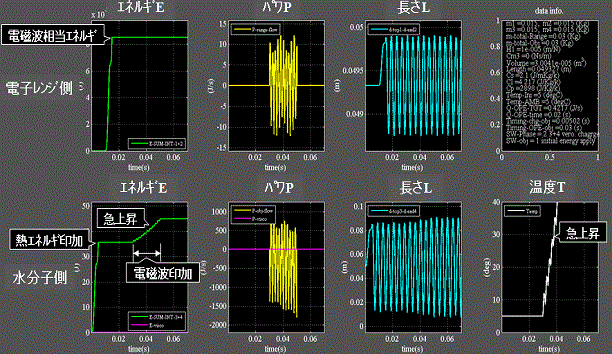
Fig.9 固有振動数と同じ速度変化を印加した場合
・下段1列目:エネルギは急上昇する。
・下段4列目:温度は急上昇する。
|
*1:物理の教科書では、力の作用~反作用の原理と書かれている。
普通、力は加えるものという概念を持っているが、現実に加えているのは速度であり、その結果として復元力が返ってくる=手応えを感じるのである。
レーザー医療の中にレーザーメスがあるが、力を掛けて切断している訳では無く、周波数の極めて高い速度変化を与えて切除したい組織を加振している事になる。
|
●空間の考え方
電磁気学では、電磁波は電場と磁場の周期的な空間の歪みの伝播と説明されている。
そして電子レンジの電磁波が水分子の温度を上昇させる事実から、前述のように実体の無い空間でもエネルギを伝播出来る事を示している。
一方、アインシュタインの一般相対性理論では質量mが存在すれば周囲の空間が歪むと表現されている。
そして、そうした空間(状態)を重力場と呼んでいる。
空間という表現には実体が有るものと、無いものを同時に含んでいるように思う。
電磁波が電場と磁場の振動と言っても実体は無く、空間の歪みも同様である。
質量mの存在と言えば原子や電子からブラックホールのような巨大な質量を持った天体まで実体があり、そこにはニュートンが万有引力と呼んだ近接作用が存在する。
質量mが存在するならば、自ずとそこに実体が無ければならない。
このように考えて筆者は以下のような見方をした。
・空間には実体が有るものと無いものがある。
・どちらもエネルギを蓄え、伝播する機能を持つ。
・実体の無い電磁波の電場と磁場は対になっており、両者は切り分けられない。
・これに倣えば、実体の有る物質が存在すれば、そこには重力場と、その対となる場がある筈である。
・重力場の対になるものとして "バネ場" という物を考える。
・"重力場" と "バネ場" は、"その法則が成立する場" と言う意味で "ニュートン場" と "フック場" と呼ぶ事も出来よう。
・両者は切り分けられない。
・空間に外から直接作用出来るのは
・力学:速度v
・電磁気学:電圧V
・空間に生じるものは、
・実体が有る場合:運動と変形
・実体が無い場合:重力場とバネ場、及び電場と磁場
・エネルギが伝播される現象を扱う場合、
・実体が有る場合:力学
・実体が無い場合:電磁気学
これらをまとめたのが、表1である。補足資料10にも説明あり。
注:実体の有る空間=物質、実体の無い空間=量子力学や電磁気学で言われる真空を意味する。
| 空間 |
| 実体有り |
|
|
| 実体無し |
|
| 電場 |
電圧V |
静電容量C |
静電エネルギ |
アンペア
マックスウェル |
|
| 磁場 |
電流I |
インダクタンスL |
電磁エネルギ |
ファラデー
|
|
| 電磁波 マックスウェル |
|
| 量子力学 |
| 近接作用 | 万有引力(ニュートン) | クーロン力(クーロン) |
以上から、本報の電子レンジのモデルは実体の無い現象を扱う電磁気学を用いず、実体のあるバネに置き換え、実体のある現象を扱う力学で表現したものと言える。
電磁気学の磁場に相当するものとして筆者は力学にバネ場という見方を加えた。
この "場" と言うものを "機能" と捉えると、
・重力場の機能:物質の質量mが加速度=速度差v=運動を生じさせる。
・電場の機能:コンデンサの静電容量Cが電位差Vを生じさせる。
・バネ場の機能:物質の柔性Hが復元力F=変形(変位)を生じさせる。
・磁場の機能:コイルのインダクタンスLが電流Iを生じさせる。
実体のあるバネを考えると、伸縮している状態はバネ両端に速度差vが生じており、同時にバネ内部には復元力Fが発生している事から、ニュートンの運動の法則とフックの変形の法則は切り分ける事は出来ないという見方が出来る。
これが運動と変形(伸縮)、速度vと力F、重力場とバネ場、電圧Vと電流I、電場と磁場が対になっている=双対性である。
ド・ブロイは1924年に物質波=万物は振動しているという概念を提唱したが、伸縮と言う概念があったかどうかは定かでは無い。
これに関しては補足資料●量子力学の波動方程式との対比を参照されたい。
|
●電場と重力場について
電場と重力場は実体が無いので、なかなかイメージ出来ない。
Fig.9に示したように、物質を構成する分子にその固有振動数に等しい振動数を持つ電磁波を照射すると、電場の振動に共振して分子の振動が励起される。
これを分子が電磁波を吸収したと表現する場合がある。
そして、吸収する振動数の違いを吸収スペクトルと呼び、物質に含まれる分子(元素)の特定や分子自身の構造解析に応用されている。
これは分子を構成する原子の種類(電子配置)に応じた電荷の偏りが、電場の振動によって励起されるものである。
また励起現象から逆に、分子はバネのように伸縮すると言うモデルが提言されている。[2]
以上から、電場と重力場は空間を励起させるポテンシャルを持った状態=電荷Cと質量mを備えた状態と表現出来る。
|
●磁場とバネ場について
磁場とバネ場も実体が無いので、同様にイメージ出来ない。
ただ、磁場はコイルに電圧を印加すると磁力が発生する事で少しイメージし易いかもしれない。(小学校の理科の実験)
これは、実体の有るバネに速度を印加すると内部に復元力が生じる事に倣えば、コイル内部の実体の無い空間に生じた復元力が磁力と解釈出来る。
一方、ニュートンが万有引力と呼んだので我々はそこに力が生じているように解釈しているが、アインシュタインによれば忽然と力が生ずるのではなく、生じているのは空間の歪みであり、筆者はこれをバネ場と呼んだ。
これは次のような見方をすると判りやすい。
地球上でバネを垂直に吊るした時、バネの全長は自身と地球の質量、およびお互いの重心間距離に因って決まる長さまで伸びる。
この時、バネ内部に生ずる復元力は重心に作用する重力=万有引力と釣り合っているから万有引力とは復元力に他ならない。Fig.10参照
つまり、空間の歪みとは柔性Hを備えたバネが伸びた状態に他ならない。
以上から、磁場とバネ場は磁力と復元力が生じた状態と表現出来る。
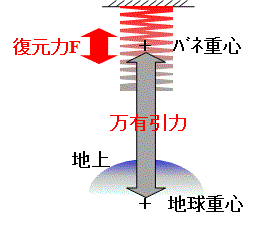
Fig.10.
|
ところで、復元力が生じた状態とは人に適切な言葉を掛けると気力がみなぎってくる=オーラを発する状態に似ている。
逆に掛けた言葉でストレスが生じてしまった場合はパワハラになるかもしれない。
ストレスも殺意にまで昇華すると殺気を放つと考えれば判りやすい。
どんなに高いポテンシャル(電場、重力場)を持っていても人は言葉(速度印加)次第で結果を出す事もあれば、出せない事もあると考えれば良かろう。
なお、オーラについては既研究ノート 重力発現モデルでも取り上げているので参照されたい。
ニュートンが万有引力の法則を発表した時、フックは同じ概念は自分が先に考えたと反論しており、ニュートンは復元力という見方をしていない点に異議を唱えたものと思われる。
そもそもニュートンは万有引力が何であるかは問うておらず、二つの物質の質量m、及びその距離Lと力についての関係式を導いただけである。
二人の間にあるのは見方の違いと言えるが、二人はこれを機に事ある毎に対立するようになった。
これは二人の内部にストレスが生じた証左と言える。
フックの死後、ニュートンは彼の書物や実験装置、肖像画まで焼却してしまったと伝えられている。
ストレスもここまで来ると怨念と言えば良いだろうか?
|
●重力波について
前段の電子レンジの物理機能モデルの中で、"電磁波が 実体の無い空間を伝播するのは判るが、実体のあるバネが物理的に結線されていないのに、どうやって速度を伝える事ができるのか?"と言う疑問を残した。
結論から先に述べると、重力波によって伝わるのである。
表1に示したように、実体が無い空間について以下のように考える。
・電磁波の源は電場と磁場の振動であり、実体が無い。
・重力波の源は運動と変形によるバネの伸縮であり、実体が有る。
・実体が有る物質はド・ブロイが示すように振動している。
・物質はその最小単位である原子、分子の連鎖だが、原子、分子間距離はゼロではない。
・実体が有る物質は実体の無い空間=空隙を内在している。
・物質はスポンジのように原子と空隙はお互いに隣接して伸縮している。
・これは入れ子構造と言える。
このように考える事で、片方のバネ端部の速度が実体の無い空間を介して他方のバネ端部に伝わるのである。
つまり、一個の原子から宇宙全体に至るまで入れ子構造になっていると言える。
既研究ノート 重力発現モデルでは、二つのバネに挟まれた実体の無い空間までモデル化しているので参照されたい。
そこでは重力波をバネ端部速度と復元力のリサージュ波形として可視化しているが、本報のFig.5がそれに相当する。
現実の重力波は2016年に初めて観測されたが、連星のブラックホールが衝突した結果と分析がなされたようにこれも実体の有る物質を源とする実体の無い空間の歪みである。
極めて微弱なものであり、特別な観測設備と天文学的なチャンスに恵まれないと観測されないと予測されていた。
本報で述べる重力波は机上実験でズームされたものと言える。
例えば、自動車のサスペンションのバネが伸縮しても重力波は生じていると解釈出来る。
|
●速度=外延量と力=内包量について
”力学的に物質を操作出来るのは速度=外延量だけであり、力=内包量は物質内部に生じる“ について、本報の電子レンジモデルを用いてこれを検証した事例を示す。
検証方法として、水分子側のバネを伸縮させるのに、速度を印加した場合と力を印加した場合の違いを確認する。
まず、Fig.11_1~2に速度を印加した場合を示す。

Fig.11_1
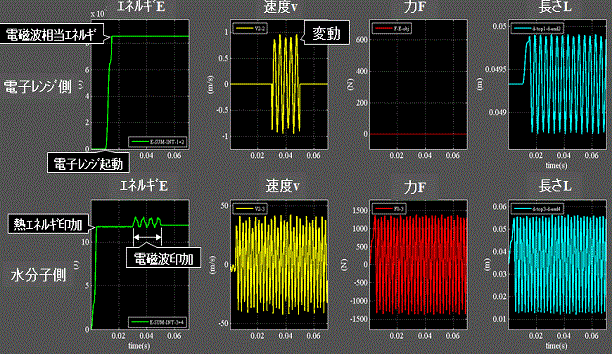
Fig.11_2 印加方法の違い 速度印加の場合
・2列目上段:電子レンジ側のバネ右端に生じる速度変化を水分子左端に印加する。
・水分子に印加する速度vは時間に対する変動量となる。
・1列目下段:水分子側のエネルギ波形は加振されて不規則である。
|
次に、Fig.12_1~2に力を印加した場合を示す。

Fig.12_1
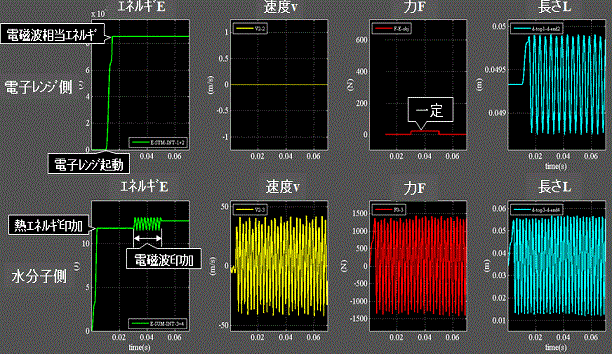
Fig.12_2 印加方法の違い 力印加の場合
・力を印加するには先述の Er = Ef = 1/2 H・f2の関係を用いて電子レンジ側のバネに蓄えられているエネルギErから力fを取り出す。
・この時、力fは時間に依存しない一定量となり、電子レンジ側のバネの伸縮とは無関係に、水分子側のバネ内部=重心に直接、力fを印加する事になる。(モデルゆえに可能なバーチャルな印加である)
・3列目上段:力一定で印加するので加振にならない。
・1列目下段:水分子側のエネルギ波形は規則性がある。
|
以上から、実体の無い空間の歪みは力=内包量ではなく速度=外延量に因って生じる事が確認できる。
電磁波で言えばエネルギは磁場ではなく電場によって伝搬されると言える。
|
●速度変化を印加するタイミングについて
本報のパラメータは電磁波印加時刻を0.03秒としたが、0.0295秒では水分子の温度上昇量が異なる例をFig.13に示す。
これは電磁波印加時刻=加振タイミングが、水分子側バネが伸び過程にあるか?縮み過程にあるか?で異なるからである。
互いに縮み側と伸び側で逆向きになった場合はカウンタパンチとなってパワは加勢されるが、同じ方向になった場合はパワは去勢=削がれる事になる。
これは前述のように実際の電子レンジの電磁波周波数が2.4GHzであるのに対し、本モデルに於ける固有振動数は電子レンジ側バネ:312.50Hz、水分子質側バネ:142.86Hzと低い為にエネルギ振幅は反比例して大きくなり、差異が拡大されたものと考えられる。
実際の電子レンジでは電磁波を印加するタイミングの違いによる差異は観測出来るオーダーにはなく、埋もれてしまうと言える。
この現象は水ヨーヨーを振るタイミングによって上手く振れたり振れなかったりするのと同じである。
前述のように、"どんなに高いポテンシャル(電場、重力場)を持っていても人は言葉(速度印加)次第で結果を出す事もあれば、出せない事もある" と同じである。
なおこの詳細は既研究ノート ド・ブロイ波の力学的解釈、及び浮遊する柔らかい物質の振動解析でも触れているので参照されたい。
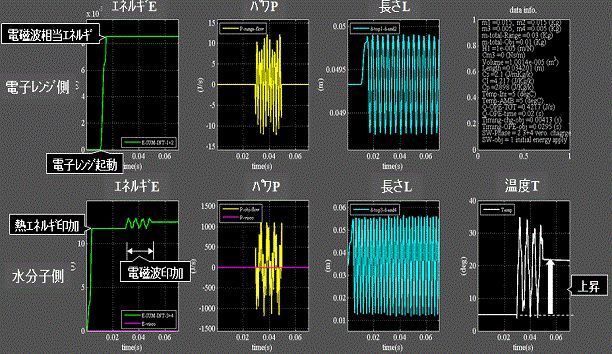
Fig.13. 電磁波印加時の物理量観察 印加時刻:0.0295秒
・下段4列目:Fig.4と比べて温度の上昇度合いが異なる。
|
|
●タイミングと量子もつれについて
タイミングを計ると言う操作は日常、良く見られる。
駅でエスカレーターに乗る際やホームから電車に乗り込むような場合に他人との間合いを計っていると言える。
これが上手くいかないとお互いにストレスを感じる。
民族間のストレスが戦争に発展してしまうのは励起現象と言えるかもしれない。
量子力学では量子もつれという状態が研究されているが、近年、電子のスピンの向きを操作する手法が確立された事で量子もつれ状態を任意に作り出せるようになった。
これは二つの電子のスピンの向き=振動のタイミングをお互いに揃える事である。(3次元方向である)
従来はスピンの向きがランダムな状態を確率的に扱ってきたが、一方を揃えれば片方の電子の電荷+-の向きが自律で揃う事になり、この原理が量子コンピューターに応用されている。
量子力学では電子自身がスピン=自転するモデルとしているが、物理機能モデルのように物質を質量mと柔性Hを持って伸縮するというモデルでもタイミングを計るという事は同じである。(本報では1次元方向である)
|
もくじへ戻る
 まとめ
まとめ
| ・ |
柔らかい物質の物理機能モデルを用いて電子レンジの電磁波と水分子を実体の有るバネで表現した。
|
| ・ |
電子レンジ側のバネの伸縮から実体の無い空間の歪みが生じ、それが伝播して隣接する水分子側バネを伸縮=励起させる現象を模擬出来た。
|
| ・ |
伝播しているのは単位時間当たりのエネルギ(Js-1)、すなわちパワである。
|
| ・ |
伝播したパワの時間積、すなわちエネルギ(J)によってバネ(水分子)が蓄えるエネルギが増加し、温度の上昇となって現れる事を示した。
|
| ・ |
本報の電子レンジのモデルは実体の無い現象を扱う電磁気学を用いず、実体のあるバネに置き換え、実体のある現象を扱う力学で表現したものと言える。
|
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
[2]:赤外吸収スペクトルと分子構造研究一バネと玉の振動から形を推測する 岡本裕巳 著
化学と教育 47巻1 号 1999 年 P42
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・赤外吸収スペクトルと分子構造研究一バネと玉の振動から形を推測する 岡本裕巳 著 化学と教育 47巻1 号 1999 年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 物質の柔性が粒子と波動性に及ぼす影響
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 気体の物理機能モデル
研究ノート パウリの排他原理のモデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 





















