研究ノート
気体の物理機能モデル
2025.8.25
五十川晋一
|
 目的
目的
気体ではボイル・シャルルの法則
| P・V = n・R・T (P・V) / (R・T) = m / M = cons. |
n:モル数 R:気体定数 m:質量 M:モル質量 |
(1.1) |
が成り立っているが、これは圧力P、体積V、絶対温度Tの関係を表しているだけである。
例えば、気体を圧縮すると温度が上昇し、膨張させると降下するメカニズムは問うていない。
ボイル・シャルルの法則はエネルギ保存則とも言えるが、
・上式の左辺の、圧力P(Pa)or(Nm-2)と体積V(m3)の積はエネルギE(Nm)or(J)である。
・上式の右辺の、温度T(k)は熱力学に於いては熱エネルギの一種と言われている。
・しかしながら、単位は(J)と(k)と言うように異なっている。
一方、熱エネルギE = P・V(J)と温度T(k)の比をとったものを、E / T = エントロピS(Jk-1)と表している。
ここで、S = n・Rでもあるが、右辺はモル数が決まれば一定の値であるのにエントロピSは様々に変化するという奇妙な?関係にある。
また、エントロピは説明が難しく様々な解釈が出来るので熱力学以外の統計力学、情報理論、経済学でも登場する。
こうした背景には、熱エネルギと呼んでいるものが力学的には何なのか? ある種の曖昧さがあるように思われる。
本報では柔らかい物質の物理機能モデルを用い、前述のメカニズムを構築して考察する。
これは物理的に熱エネルギの出入りを見えるようにする課題と言える。
なお、ボイル・シャルルの法則は理想気体について当てはまるが、実在気体について適応する場合は近似的なものになると言われている。
これは理想気体とは気体分子を点と見なし(大きさを持たない)、かつ完全剛体と見なしている事に因るものである。
物理機能モデル手法では物質は大きさを持ち、完全剛体と見なさない、すなわち剛性k=バネ定数を持つとしているのでボイル・シャルルの法則からずれた結果が得られる事が予想される。
なお、物理機能モデル手法の詳細は補足資料に示した。
 もくじ
もくじ
●柔らかい物質について
●机上実験
・気体(物質)の物理機能モデル
・パラメータ
・試験条件
・結果
●考察
・固体、液体、気体の見方
・見かけの体積が変化するバネ
・速度エネルギ、力エネルギ、熱エネルギの関係
・モル数n、気体定数Rと柔性Hの関係
・理想気体と実在気体の扱い方
・力学の双対性
・エントロピについて
・理想気体と一般相対性理論、物理機能モデルの関係
・物理機能モデルの適応範囲
・統計モデルと物理機能モデル
●まとめ
●参考文献
 柔らかい物質について
柔らかい物質について
Fig.1参照
物質は点ではなく、長さ(空間)を持つ。
密度は均一ではなく、質点(重心)は物質内を移動する。
力fは質点に作用する=ニュートンの運動の法則
復元力fiは相対速度vrによって生じる=フックの変形の法則
物質は変形=伸縮しながら運動する。
これは物体全体が運動するか否かに関わらず、物体内部で質点が運動していると言う事である。
柔らかさ=柔性とは剛性の逆数であり、相対的なものである。
物質の質量に対して相対的な柔らかさという意味である。
こうした見方をする時、物質は粒子と波動の性質を併せ持つ。[1]
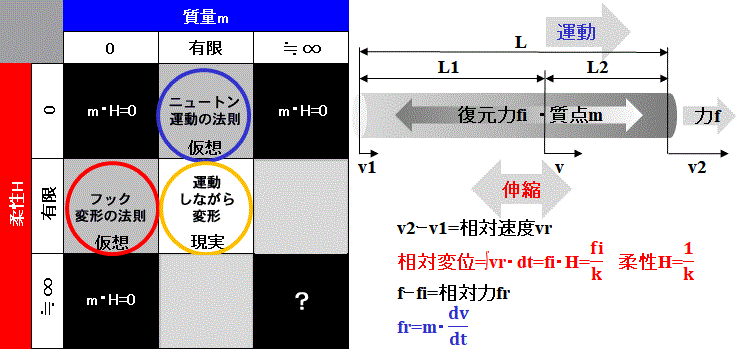
Fig.1
|
もくじへ戻る
 机上実験
机上実験
●気体(物質)の物理機能モデル
Fig.2にモデル図を示す。
基本モデルは柔らかい物質を模擬したものであり、一次元方向に伸縮するバネと考えて差し支えない。
机上実験用モデルはそれを4連にしたもので1個のモデルは1モルの分子の集合を表す。
注:物質の両端部は固定、解放が操作出来る
注:エネルギ消費要素である粘性抵抗係数C、塑性抵抗係数Dはゼロとしてある
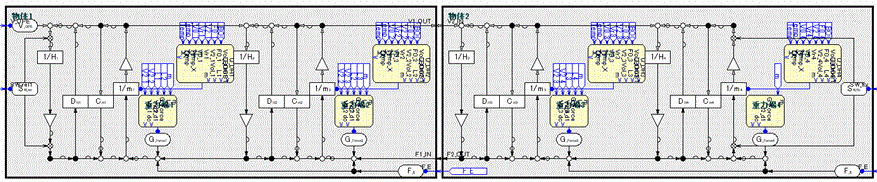
 Fig.2
Fig.2
|
|
●パラメータ
・質量m:0.02801(kg)×4 (窒素分子N2 4モル分とする)
・柔性H:1.0e−3、1.0e−4、1.0e−5(mN−1)の3水準 (剛性kの逆数)
・モル比熱(定圧)Cp:28.0(Jmol-1k-1)
・モル比熱(定積)Cv:Cp - R(Jmol-1k-1) R:気体定数=8.314
・初期圧力:1.013e5(Pa)= 1気圧
・初期体積:0.099(m3)
・初期温度:20 + 273.15(k)(20℃)
・初期熱エネルギ:上記パラメータに於いて9749.00(J)
|
●試験条件
・物質に初期熱エネルギを印加して自由振動させる。 印加方法は考察の中で説明する。
・case1:圧縮膨張(容積変化):左端速度±1.0e1(m/s)正弦波周期1.0(s)
・case2:加給除給(容積一定):±1.0e-2(m3/s)正弦波周期1.0(s)
・case3:加熱(容積一定):0→1.0e4(Js-1)線形暫増
・case4:加熱(容積変化):0→1.0e4(Js-1)線形暫増
・サンプリング時間:0.1msec
・なお、加熱以外は熱伝達の無い断熱条件下とする。
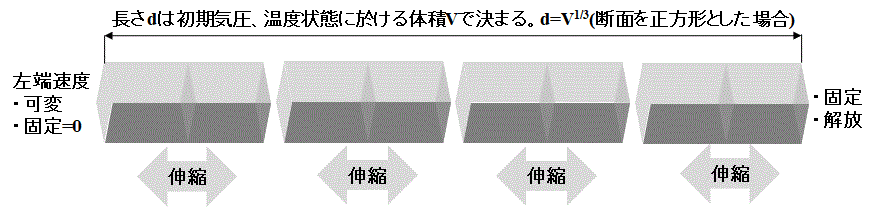
Fig.3
|
|
●結果
|
Fig.4に気体分子に初期熱エネルギを印加する過程を示す。 柔性H=1.0e-3
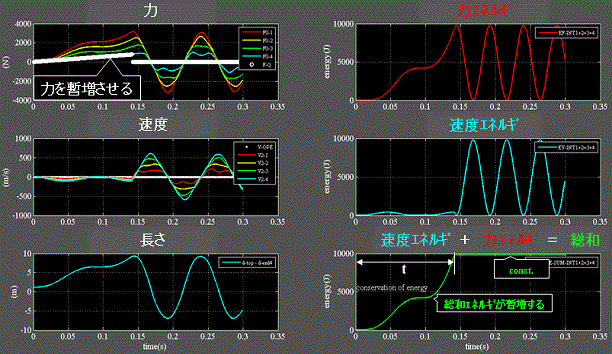
Fig.4
・左上:初期熱エネルギと等価な力を0から暫増させる。(白プロット)
・左下:分子は自由振動を始める。
・右下:速度エネルギ+力エネルギの総和が熱エネルギEに達したら力の暫増を終了する。
・初期熱エネルギ印加に要した時間t=0.0213(s)
・振動中は総和=const.が成り立っている=エネルギ保存則。
|
Fig.5に気体分子に初期熱エネルギを印加する過程を示す。 柔性H=1.0e-4
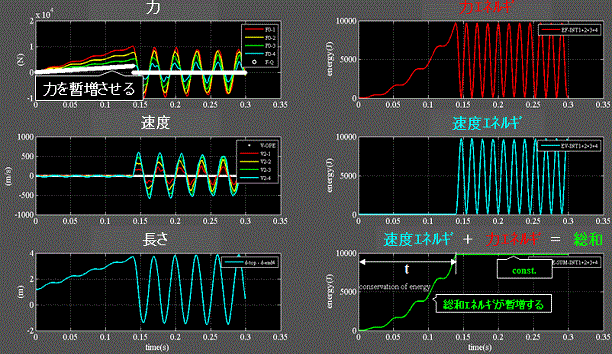
Fig.5
・右下:分子の柔性Hを減少(剛性増加)させると固有周期は短くなり、その様相が総和エネルギの上昇過程に現れる。
・但し、最終の総和エネルギは9749.00(J)で変わらない。
・柔性Hを減少させれば供給すべき力Fは、力エネルギE=1/2H・F2 の関係から自ずと増加する事になる。
・初期熱エネルギ印加に要した時間t=0.0130(s) Fig.4とは僅かに異なる。
|
Fig.6に気体分子に初期熱エネルギを印加する過程を示す。 柔性H=1.0e-5
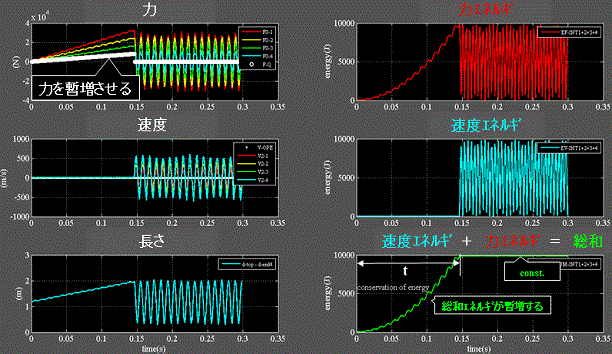
Fig.6
・右下:分子の柔性Hを減少(剛性増加)させてもFig.5と同様に最終の総和エネルギは9749.00(J)で変わらない。
・初期熱エネルギ印加に要した時間t=0.0141(s) Fig.4~5とは僅かに異なる。
|
Fig.7に自由振動状態の観測結果を示す。 柔性H=1.0e-5
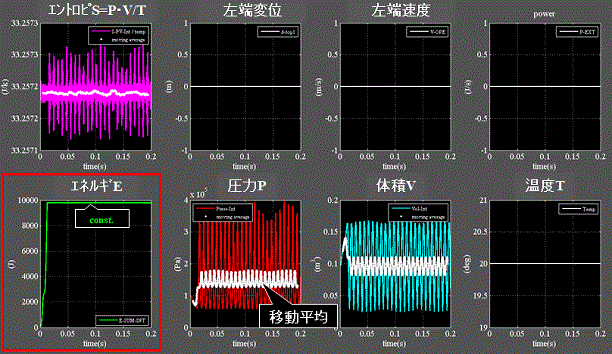
Fig.7
・下段1列目:初期熱エネルギが速度エネルギ+力エネルギ=const.として蓄積されている事を示す。
・下段2、3列目:気体分子は伸縮により圧力P、体積Vは変動するが、移動平均(白プロット)を取ると ”ほぼ” 一定。
・ ”ほぼ” の意味は、モデルはバネを4連にしているので非線形となり、振幅は正弦波ではなくゆらいでいるゆえ。
・上段1列目:エントロピSも微小にゆらいでいるが、移動平均は同様である。
|
Fig.8に自由振動状態に於ける P・V=n・R・Tの関係を確認した結果を示す。 柔性H=1.0e-5
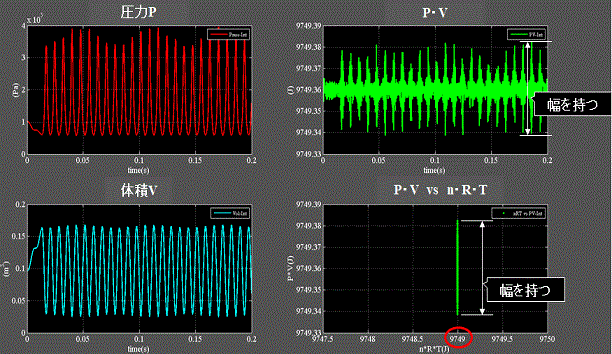
Fig.8
・左上、左下:気体分子は伸縮により圧力P、体積Vは変動する。
・右上:両者の積P・Vも変動する。
・右下:理想気体について成り立つボイル・シャルルの法則では温度20℃に於けるn・R・T = 9749.00(J)だが、P・Vの値は一意に定まらず、微小にゆらいでいる=幅を持っている事が判る。
|
Fig.9にcase1:圧縮膨張(容積変化)の結果を示す。柔性H=1.0e-5
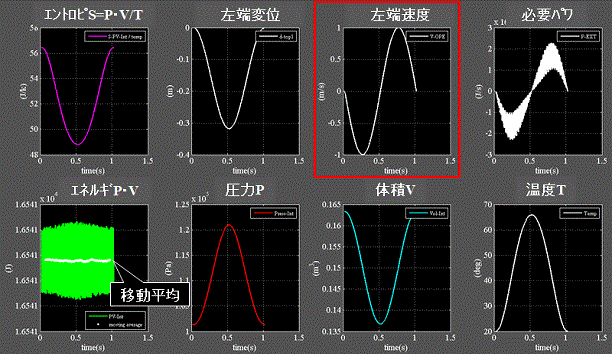
Fig.9
・コンプレッサのように気体を閉じ込めた剛なる容器の容積を変化させる例である。
・上段3列目:操作量は左端の速度としている。
・上段2列目:左端の変位量を示す。
・上段4列目:圧縮膨張に必要なパワを示す。 これが気体(物質)の温度を変化させる。
・下段1列目:気体(物質)に蓄積されているエネルギP・Vはボイル・シャルルの理想気体の様に一定にはならない。
・上段1列目:エントロピSは温度TとエネルギP・Vの変化に応じて上下する。
|
Fig.10にcase2:加給除給(容積一定)の結果を示す。柔性H=1.0e-5
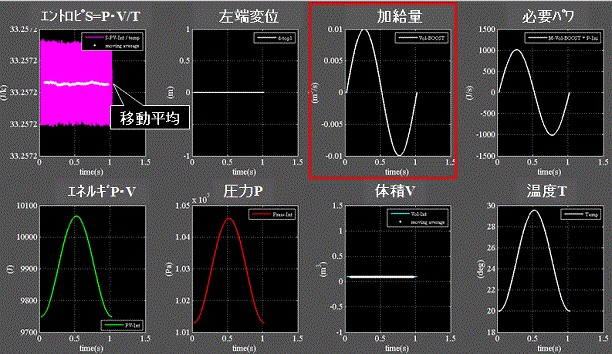
Fig.10
・圧搾エアタンクのように容積一定の剛なる容器内に気体を押し込み~吸い出す例である。
・上段3列目:操作量は時間当たり加給量=体積(m3s-1)としている。
・上段4列目:加給除給に必要なパワを示す。 これが気体(物質)の温度を変化させる。
・下段1列目:気体(物質)に蓄積されているエネルギP・Vは外部からのパワに因って変化した事を示している。
・上段1列目:膨張が阻止されるのでエネルギP・Vは上下するが温度Tも上下するのでエントロピSはほぼ一定である。
|
Fig.11にcase3:加熱(容積一定)の結果を示す 柔性H=1.0e-5
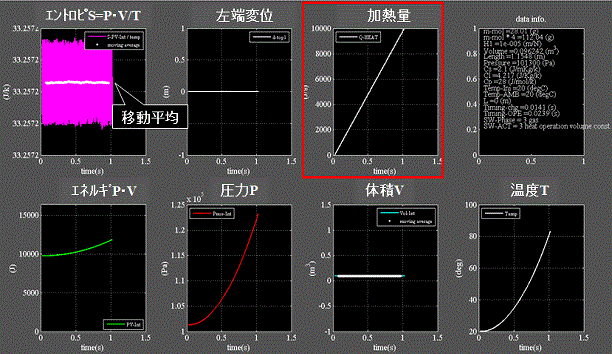
Fig.11
・容積一定の剛なる容器内の気体を外部から加熱する例である。
・上段3列目:操作量は加熱パワ(Js-1)としている。 これが直接、気体(物質)の温度を変化させる。
・下段1列目:気体(物質)に蓄積されているエネルギP・Vは外部からのパワに因って変化した事を示している。
・上段1列目:膨張が阻止されるのでエネルギP・Vは上昇するが温度Tも上昇するのでエントロピSはほぼ一定である。
|
Fig.12にcase4:加熱(容積変化)の結果を示す 柔性H=1.0e-5
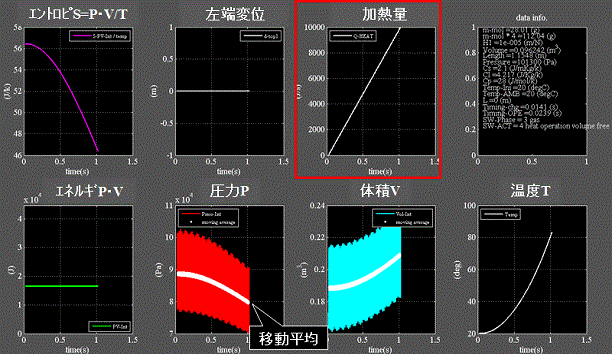
Fig.12
・蓋の無い容器内の気体を外部から加熱する例である。
・上段3列目:操作量は加熱パワ(Js-1)としている。 これが直接、気体(物質)の温度を変化させる。
・下段1列目:気体(物質)に蓄積されているエネルギP・Vは一定を保っている。
・上段1列目:解放状態の気体はエネルギP・Vは一定だが温度Tが上昇するのでエントロピSは降下している。
|
Fig.13にcase1に於いて圧縮タイミングを変えた結果を示す t = 0.0239秒 膨張側から操作開始。
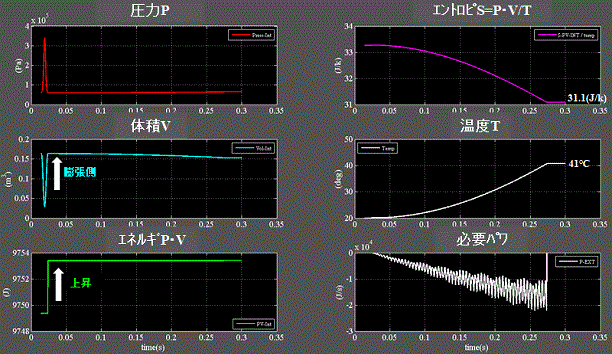
Fig.13
・中段左:自由振動中の気体の体積Vが膨張側=コンプレッサの下死点から操作開始すると、
・下段左:エネルギ=P・Vの値は上昇し、
・中段右:最終温度は41℃。
・下段右:下死点では気体の復元エネルギは縮み方向に働き、外部から流入するパワが同じ方向だが気体の縮み速度が圧縮操作より速いので気体の方が逃げる=仕事をされる側になる為、必要パワは負となる。
・上段右:最終エントロピSは31.3(Jk-1)。
|
Fig.14にcase1に於いて圧縮タイミングを変えた結果を示す t = 0.0286秒 圧縮側から操作開始。
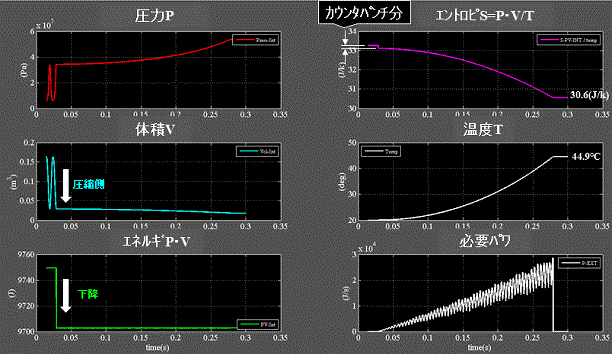
Fig.14
・中段左:自由振動中の気体の体積Vが圧縮側=コンプレッサの上死点から操作開始すると、
・中段右:エネルギ=P・Vの値は下降し、
・下段左:最終温度は44.9℃。
・上死点では気体の復元エネルギは伸び方向に働き、外部から流入するパワは逆方向の為、気体に仕事をする側になる。
・上段右:これはカウンタパンチになり、Fig.13で膨張側から圧縮操作をするより最終エントロピは30.6(Jk-1)と低く、最終温度は高くなる。
・下段右:これは圧縮に必要とされるパワ、エネルギが効率的に気体温度上昇に使われたと解釈出来、必要パワは正となる。
|
|
もくじへ戻る
 考察
考察
●固体、液体、気体の見方
柔らかい物質の物理機能モデルを用いて気体を表現した訳だが、身近な例では空気の抜けた自動車のタイヤに再充填すれば車体が持ち上がる。
nモルの気体の分子は体積は定まらないが以下のエネルギを蓄えている。
| Et = n・R・T Et:熱エネルギ、n:モル数、R:気体定数、T:温度 |
(1.2) |
体積が定まらないと言う事は逆に、膨張すればこの熱エネルギで外に対して仕事が出来る。
これは熱力学的な見方である。
一方、質量や体積を持つ固体や液体は溶鉱炉のような余程の高温でなければ日常的には熱エネルギを蓄えていると見なさなくとも実害は無い。
これは機構力学や流体力学的な見方である。
固体、液体は自律で体積が決まっているので静止している限りは外に対して仕事は出来ないが、例えば砲弾や高圧洗浄機のように物質に速度を与えることで速度(運動)エネルギを蓄えさせると仕事が出来る。
また固体であってもバネはその形状を成している実体部分の体積は変わらないが、両端間の距離が変化=伸縮するので見かけの体積(密度)が変化する物質と見なす事が出来る。
物理機能モデルでは固体もバネ剛性を持っており、伸縮しながら体積が変化する事によって外に対して仕事が出来るという見方をすれば、気体と同じ扱いが出来る。
タイヤはジャッキにもなると言う事である。
|
●見かけの体積が変化するバネ
|
上述のように固体、流体、気体の別無く、物質を見かけの体積が変化するバネと見なせば、以下のエネルギを蓄える事が出来る。
| Ev = 1/2 m・v2 Ev:速度(運動)エネルギ、m:質量、v:バネ端部速度 |
(1.3) |
| Ef = 1/2 H・f2 Ef:力(変形)エネルギ、H:柔性、f:バネ復元力 |
(1.4) |
| E = Ev + Ef = const. |
(1.5) |
上式は力学の双対性を現し、式(1.5)は対になったエネルギの和は常に一定となる事からエネルギ保存則と呼べる。
また、物質を実体があるか無いかは別にして両端間の距離=長さを持つ空間と見なす事が出来る。
気体が漂っている空間とは真空の中に無数の分子という実体が存在している状態と言う見方が出来る。
気体が漂っていない真空の宇宙空間には無数の天体という実体が存在していると言う見方も出来る。Fig.15参照
こうした見方をすると、空間は入れ子状となって伸縮すると言える。
この状態は数学的には自己相似=フラクタルと呼ばれ、部分の構造が全体の構造と相似の関係にある。補足資料5参照
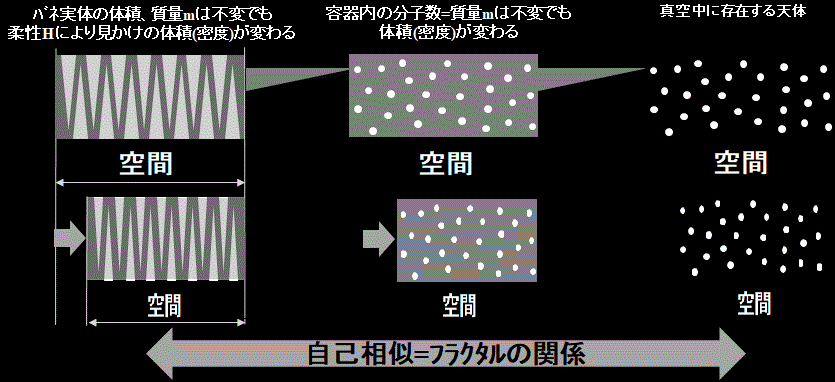
Fig.15.
|
|
●速度エネルギ、力エネルギ、熱エネルギの関係
気体が蓄えている熱エネルギだが、Fig.4~6で述べた物理機能モデルに供給する方法に沿って考察する。
物理機能モデルで表される物質は外部からエネルギを供給しない限り静止状態を維持する。
これは物質(空間)は現状のエネルギを維持しようとし、変化があれば元に戻ろうとする=エネルギ保存則と言える。
nモル分の気体は質量を持っているが、絶対零度0(k)= -273.15℃以上の温度T(℃)では熱エネルギEtを蓄える。
本報では初期状態を4モル、温度 = 20(℃)= 293.15(k)としているので、 R:気体定数=8.314を用いて、
熱エネルギEt = 4×8.314×293.15(k)= 9749.00(J)
これを最初に物理機能モデルに供給する必要があり、方法を補足資料9に示す。
この操作は万有引力(重力)が働く地球上で物質(バネ)の上端を固定して高さh(m)に吊り下げる事に相当する。
この時、バネの自由長は伸び、物質内部には復元力が生じ、力エネルギを蓄え、高さhとは重心の位置である。
逆に言えば、物質を柔らかいと見なす場合、力エネルギとは地球と物質の位置によって決まる位置(ポテンシャル)エネルギと言える。
以上のように、物質は伸縮する事で熱エネルギEtは力エネルギEfと相互に変換可能となり、熱エネルギEtを蓄えたnモルの気体分子が物理機能モデル=バネ上に表現される。
逆に言えば、力エネルギEfが蓄えられるには物質は運動するだけではなく振動、それもスピン(自転)では無く、伸縮が必要になり、物質は質量mと柔性Hを共有していなければならない。
これが冒頭のFig.1で述べた、物質は点では無く完全剛体でも無い、の意味である。
スピンの場合、スピンに角速度があるとするならば直進運動と同じく質量mに蓄えられるエネルギは速度エネルギEvゆえ、力エネルギEfは生まれないので、式(1.5)=エネルギ保存則は成り立たない。
なお、理想気体では通常、内部エネルギUと呼んで以下のように示されている、
| 単原子気体の場合:U = 3/2n・R・T |
(1.6) |
| 二原子気体の場合:U = 5/2n・R・T |
(1.7) |
U = 分子の運動エネルギEk + 分子間力によるポテンシャルエネルギEp
| U = Σ(1/2m・v2 + ϵ内) + Σ(Ep) |
(1.8) |
ϵ内:H2 、 N2等の2原子分子やH2 Oのような多原子分子の自転,または分子間距離の伸縮による振動運動で生じる。
ここであらためてエネルギについて理想気体と物理機能モデルで扱う実在気体の見方の違いを以下に整理しておく。
|
エネルギU
|
運動エネルギEk = (1/2 m・v2 + ϵ内)
+
ポテンシャルエネルギEp
|
エネルギE
|
運動エネルギEv = 1/2 m・v2
+
力エネルギEf = 1/2 H・f2
+
熱エネルギEt = P・V = n・R・T
|
|
・分子を大きさを持たない質点と見なしているのに "分子間距離" を持ち出している
|
・分子は点、完全剛体とは見なさず伸縮する。
・力エネルギは位置(ポテンシャル)エネルギと言える。
|
次に一般力学と熱力学に於ける物理特性、物理量、エネルギを対比させると以下の表1になる。
| 表1 |
一般力学
|
熱力学
|
| 物理特性 |
| 質量m(Kg) |
| 柔性H(Nm-1) |
比熱C(JKg-1k-1)
XXX-1 |
|
| モル数n(mol) |
| 気体定数R(Jmol-1k-1) |
定圧モル比熱Cp(Jmol-1k-1)
定積モル比熱Cv(Jmol-1k-1)
|
|
| 物理量 |
| 外延量 |
| 速度v(ms-1) |
体積流量L(ls-1)
質量流量M(Kgs-1) |
モル流量N
(mols-1) |
|
| 内包量 |
|
|
| 単位時間当たりエネルギ=パワ |
F・v(Nm-1)or(Js-1) |
P・L(Nm-1)or(Js-1) |
| 流入・流出エネルギ |
F・∫vdt = F・d(Nm)or(J) |
P・∫Ldt = P・V(Nm)or(J) |
蓄積
エネルギ |
| 外延エネルギ |
運動エネルギEv = 1/2m・v2(Nm)or(J) |
| 内包エネルギ |
変形エネルギEf = 1/2H・F2(Nm)or(J)
| 熱エネルギEt = m・C・T(J) |
熱エネルギEt = n・R・T
=n・(Cp-Cv)・T(J) |
|
|
注:∫vdt=変位d(m)、∫Ldt=体積V(m3)
なお、外延量と内包量については補足資料3を参照
ここで、エネルギ保存則は次の式で表す事も出来る。
| 外延エネルギ + 内包エネルギ = const. |
(1.9) |
単位時間当たりエネルギ=パワの式の形は外延量×内包量である。
・固体、液体の場合:F・v
・気体の場合 :P・L
外部からの流入流出エネルギの式の形は外延量を時間積分した形である。
・固体、液体の場合:F・d
・気体の場合 :P・V
蓄積エネルギについては以下の関係がある。
・固体、液体の場合:熱エネルギEt:m・C・Tと変形エネルギEf は相互に変換可能(内包エネルギ同士)
・気体の場合 :熱エネルギEt:n・R・Tと変形エネルギEf は相互に変換可能(内包エネルギ同士)
エネルギ保存則という視点で見れば、ニュートン、フック、ボイル、シャルルの各法則は全て同じ意味合いである。
|
●モル数n、気体定数Rと柔性Hの関係
気体では定圧比熱Cp > 定積比熱Cv、気体定数R = Cp - Cv = 8.314の関係にあり、単位は全て(J/mol/k)である。
これは定積変化では分子自身が蓄える熱エネルギだけで外に対して仕事はしないが、定圧変化=容積変化では膨張して仕事をする分、比熱、エネルギは大きくなる事を意味している。
これは気体定数Rとは容積変化をする場合にのみ意味のある量と言える。
そうした意味では、見かけの体積が変化するバネと同じである。
熱エネルギの式をあらためて示すと、
| 固体、液体の場合:熱エネルギEt = m・C・T |
(1.10) |
| 気体の場合 :熱エネルギEt = n ・R・T |
(1.2) |
ここで固体、液体、気体に関わらず原子1個(量子)を考えた場合、原子の質量mと比熱Cは反比例の関係にあり、両者の積は常に一定となる。
従って式(1.10)の m・C は定数である。
一方、式 (1.2)の n・R も定数である。(モル数nに応じてアボガドロ数=6.22×1023の整数倍となる)
従って、固体、液体、気体を問わず、物質が蓄える熱エネルギは元素に依存せず温度Tだけで決まる量と言える。
これは1900年にプランクが示した黒体輻射に於ける光のスペクトル分布の公式においても同様である。
これらを整理すると以下の表になる。
|
|
質量mと比熱Cの積は一定
|
|
柔性Hに依存しない Fig.4~6参照
|
|
気体定数Rは一定
|
|
ここから、気体定数Rと柔性Hは共通の性質があると言う見方が出来る。
原子の質量mと、比熱C、柔性Hの関係については既研究ノート 力学の双対性から見たプランク定数で考察しているので参照されたい。
次に、気体分子を伸縮するバネと見なした場合、外に対する仕事=エネルギは復元力fによって成される事になる。
そのエネルギは、
| 変形エネルギEf = 1/2 H・f2 |
(1.4) |
フックの変形の法則: f = k・d = d / H k:剛性 = 1 / H d:変形量 から以下のように書き換えられる。
| 変形エネルギEf = 1/2 d2 / H |
(1.11) |
例えば、
Ef = 0.5、H = 1とした場合、式(1.4) からf = 1、 式(1.11) からd = 1 となる。
Ef = 0.5、H = 2とした場合、式(1.4) からf = √0.5 、 式(1.11) からd = √2となる。
つまり、同じ変形エネルギEfの値に対して、f、H、d はフックの法則が成り立つバネなら無数の組み合わせが存在する。
これは、熱エネルギは m・C と温度Tによって一意に定まるが、変形エネルギEfの内訳は定まらないと言う事である。
その理由は、表1に示したように物質をバネと見なすと運動エネルギEvと対にならざるを得ないからである。
つまり、変形エネルギEfと運動エネルギEvはお互いに相手があって初めて成り立つものなのである。
これが、式(1.3)、(1.4)、(1.5)の意味する所である。 補足資料1を参照頂きたい。
ここで、補足資料3で示したルールをあらためて以下に示す。
・外延量:速度V、運動エネルギEv等、人間が外から直接操作出来る量である。
・内包量:力 F 、 変形エネルギEf等、物質内部に生じ、人間が関与できない量である。
・但し、内包量のうち熱エネルギEtだけは例外で、加熱、冷却のように人間が外から直接操作出来る。
現実的には力Fは忽然と物質内に生じる訳では無く、バネを縮める時に与えた速度vが原因である。Fig.16参照
普通、人間はバネに力を加えたと言う見方をするが、力学的には加えたのは速度であり、バネは復元力Fを人間に返した=反力を返したと言った方が正しい。
つまり、人間が反力を感じる事が出来るのは筋肉も柔性を持ったバネだからである。
一方、バネに熱エネルギEtを蓄えさせるには速度を印加するのではなく、Fig.4~6で示したように等価な力を印加するのである。
万物をバネと見なす場合、こうしたルールが存在するのである。
 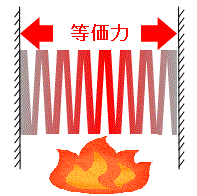
Fig.16
|
|
●理想気体と実在気体の扱い方
Fig.8では理想気体について成り立つボイル・シャルルの法則では本報の4モル、温度20℃に於いては、
n・R・T = 9749.00(J)の筈だが、P・Vの値は一意に定まらず幅を持っている事を示した。
これが冒頭のFig.1で述べた、物理機能モデルでは物質は点では無く大きさを持ち、完全剛体と見なさない=すなわち柔性を持つ事によるボイル・シャルルの法則からのずれ=誤差と言える。
この誤差を無視して良いか否かは課題に応じて決まるであろう。
なお、物質をコイルバネのように断面積が変化せずに一方向に伸縮すると仮定すれば、見かけの圧力Pは物質の復元力Fと体積Vから、面積A = V2/3 P = F / A として表現する事が出来る。
あらためて、P・V = F・V1/3 = F・d = エネルギの関係にある。
整理すると、
・理想気体ではボイル・シャルルの式 P・V = n・R・T (1.1)が成り立つ。
・物理機能モデルでは前述の式 Ev + Ef = const. (1.5)が成り立つ。
これは気体の分子(物質)を点、完全剛体と見なしても、大きさ、および柔性を持つと見なしても、どちらでもエネルギ保存則は成り立つと言える。
物質を伸縮するバネと見なせばエネルギは、速度エネルギEvと力エネルギEfに分配されると言う事である。
気体についてのボイル・シャルルの法則も物理機能モデルも課題に応じて使い分ければ良いと言える。
|
●力学の双対性
古典力学や初期の量子力学では物質を点、完全剛体と見なしているが、例えば電子を大きさと柔性を持ち、前述の様にスピンではなく伸縮すると見なせば扱い方は変わって来る。
すなわち物理機能モデル手法は物質の最小単位を扱う量子力学から天文学まで、それらに付随する機構、材料、流体、熱力学まで通貫して扱えるのである。
これは補足資料に示すように物理機能モデルが力学の双対性を踏まえたモデルゆえである。
あらためて、以下に力学の双対性の要点を記す。
・速度(運動)エネルギは質量mに、力(変形)エネルギは柔性Hに蓄えられる。
・速度V(外延量)と力F(内包量)はお互いが原因にも結果にもなる=因果関係が双方向である。
・質量mと柔性Hは切り分けられない。*1
・ニュートンの運動の法則とフックの変形の法則は切り分けられない。
・物質の運動と変形=伸縮は切り分けられない。
・電磁気学では双対性がクーロン、アンペア、ファラデー、マックスウェルの諸法則で1800年代には認識されている。
・力学のニュートン、フックの法則が電磁気学の諸法則と相似になっている事を補足資料に示す。
*1:素粒子物理学では1964年に存在が予言された物質に質量を与える役目を担う素粒子=ヒッグス粒子が2012年に発見されている。
これは質量mだけでなく柔性Hを与える役目も担っていると言える。
ここで、机上実験の結果を用いて、それが電磁気学の何に相当するかを述べる。
まず、case1:圧縮膨張のケースである。
ここでは気体(物質)の一端に速度変化を与え、他端は固定して圧縮膨張(バネの圧縮引張と同じ)させる。
補足資料3、およびFig.16で示したように、物質に外部から操作出来るのは速度V(外延量)だけである。
供給する機械パワ(Js-1)を用いて温度変化が計算される。
これは電磁気学で言えばコンデンサに電圧(電位差)を印加すると静電エネルギを蓄える事に相当する。
次に、case2:加給除給のケースである。
容積一定の中に外部から加給除給するという事は熱エネルギを蓄えた気体(物質)の質量(モル数)を増減させる事であり、電車の中に体温を持った人間を詰め込むのと同じである。
容器=気体(物質)の両端は固定しているので速度V(外延量)の形で印加する事が出来ない。
補足資料3で示したように、物質に外部から操作出来る例外として加熱、冷却のように熱エネルギがある。
ここでは容器内の気体の圧力を直接変化させる事は出来ないので、代わりに操作量を時間当たり体積L (m3/s)とし、 P・V = n・R・Tに因って決まるモル数と比熱から熱エネルギ(J)の形で供給する。
Fig.4~6で示したように熱エネルギを等価な力で印加する方法を取る。
供給する加給パワ(Js-1)を用いて物質の温度変化が計算される。
これは電磁気学で言えばコイルに電流を流すと電磁エネルギを蓄える事に相当する。
次に、case3、及びcase4:加熱のケースである。
ここでは外部から気体の温度を直接操作するのではなく、操作量を熱パワ(Js-1)としてエネルギを供給する。
手順はcase2と同様に熱エネルギを等価な力で印加する方法を取る。
供給する熱パワ(Js-1)から温度変化が計算される。
これも電磁気学で言えばコイルに電流を流すと電磁エネルギを蓄える事に相当する。
|
●エントロピについて
Fig.8に於いて、温度Tが一定で、n・R・T=定数の場合でも、P・Vの値は一意に定まらず幅を持っている事を示した。
これは現実の世界では実験室の恒温槽でもなければ温度T一定はあり得ず、 n・R・Tも時々刻々ゆらいでいると言う見方が出来る。
Fig.13~14に於いて、自由振動(伸縮)している気体に対して圧縮を開始するタイミングの違いで最終エントロピSと温度Tに差が出る例を示し、圧縮に必要とされるパワ、エネルギが効率的に気体温度上昇に使われたと解釈出来る、と述べた。
これが理想気体であれば分子は伸縮はしないので圧縮を開始するタイミングによる結果に差は生じない。
つまり、現実の世界では効率と言う概念が存在すると言える。 *2
このように考えると、冒頭で触れたように様々に変化するエントロピSとは現実のゆらぎ=諸行無常の度合いを測る概念と言える。
これがエントロピは熱力学に限らず、統計力学、情報理論、経済学等でも使われる所以である。
例えば、株価は変動するから買い時、売り時にはベストタイミングが有るという事である。
*2:自動車のアイドリング・ストップ機構では再始動する際にバッテリの負担を減らすべく、最も少ないエネルギで済むようにエンジンの上死点、すなわち気体を圧縮して復元エネルギが最大の位置でピストンを停止させれば良い。
これはFig.17のように復元力Fが最大である斜面の頂上からブランコを始める事に相当する。
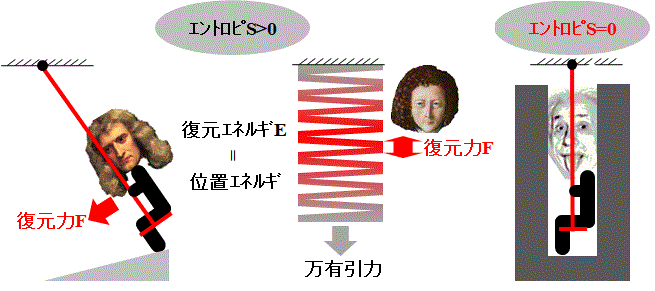
Fig.17
|
|
●理想気体と一般相対性理論、物理機能モデルの関係
Fig.4~6に於いて、物理機能モデルに熱エネルギを供給する手順を示したが、等価力Fの暫増開始から総和エネルギが0から熱エネルギに達するまでの時間tを測ると柔性Hの値に因って僅かに異なる結果が得られている。
この総和エネルギの上昇のルートは力Fの2乗に比例するので時間軸に対して基本的には二次曲線になるが、バネ自身が伸縮するのでその周期によるゆらぎを抱えている。
柔性Hを1.0e−3→1.0e−4→1.0e−5(mN−1)と小さく(剛性を大きく)してゆくとバネ自身の固有周期が短く、かつ揺らぎも小さくなり、ルートは二次曲線に近づいてゆく。
これは誤差が小さくなっていくと見る事が出来、気体分子を完全剛体と見なす理想気体に近づいたものと言える。
この時間tの誤差は物質を完全剛体と見なさず伸縮するモデルである事から生じるもので、アインシュタインが一般相対性理論に於いて表現している "時空が曲る(伸縮する)" と同じ意味合いと言える。
あるいは、"地上とスカイツリーの最上階では時間の進み方が異なる" と同じ意味合いである。
言い換えると、物質を見かけの体積が変化するバネと見なす事は一般相対性理論の見方に通じる。
アインシュタインは物質の柔性には言及していないが、仮に伸縮するバネ上の座標から観察すると周囲の座標の方が伸縮しているように見える。
彼はこれを数学的にローレンツ変換を用いて表したものと言える。
これはニュートンの運動の法則では物質を大きさを持たない質点と仮定しているのに対し、アインシュタインは大きさ(空間)を持っていると同時に、完全剛体ではなくバネのように伸縮するという見方、すなわちフックの変形の法則も頭の中には有ったのではないだろうか?
分子を大きさを持たず、伸縮しない完全剛体と仮定する理想気体はニュートンが前提とする質点と同じと言える。
なお、空間の考え方については既研究ノート 重力発現モデルで考察しているので参照されたい。
|
●物理機能モデルの適応範囲
物理機能モデルでは物質を質量mと柔性Hの対で表すので運動と伸縮(振動)が対になって現れる。
これは万物は粒子と波動の性質を併せ持つというド・ブロイの物質波と同じ見方である。
また、例えばH2Oなる水分子を考えた場合、氷、水、水蒸気というように固体、液体、気体の3相に分かれるが、どの相であっても熱エネルギを蓄えている事には変わりない。
比熱は氷:2.1(J/g/k)@-1℃、水:4.217(J/g/k)@0℃、水蒸気:2.051e3 (J/mol/k) @100℃と異なっているが、どの相でも比熱と温度によって決まる熱エネルギを持っている訳である。
このことから物理機能モデルは量子(電子)~固体物質~気体分子~熱力学上の現象まで通貫して表現する事が出来る。
万有引力は物質の柔性に応じて物質内部に生じる復元力と釣り合っている=フックの変形の法則。
同時に復元力は質量=質点(重心)に作用して物質の両端に速度差が生じる=ニュートンの運動の法則。
この双方向の因果関係によって物質=空間は伸縮しながら運動する事になる。
Fig.15に示したように、この見方は自己相似=フラクタルの性質から量子~分子~天体まで適応出来ると言える。
筆者は量子から天体に至る空間の内部では万有引力=近接作用により、分子はお互いに伸縮しながら "居場所=スタンス" を持っていると言う仕組みを考えた。
そして電磁気学の電場、磁場に倣って重力場、バネ場と表現し、Fig.18に示した。
仮にお互いの質量m、柔性Hに相対差があれば各々の "スタンス" は移動する。(下段)
これは社会の中で個々の人間がお互いにソーシャルディスタンスを保とうとする働きに似ている。
これがアインシュタインが一般相対性理論で表現した時空の曲がり=伸縮と言える。
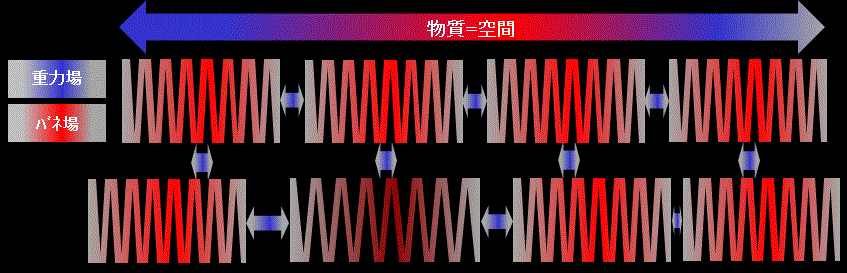
Fig.18
|
|
●統計モデルと物理機能モデル
Fig.13~14に於いて、 自由振動(伸縮)している気体に対して圧縮を開始するタイミングの違いで最終エントロピSと温度Tに差が出る例を示した。
これは時間、位置(分子の両端の)、エネルギは常に変動しており、一意に定まらないと言う見方が出来る。 *3
理想気体はひとつのモデルだが、実在気体を表現するモデルとして分子のランダムな運動や、衝突、分子間に働く力(近接作用)等を勘案し、確率の概念を導入した統計モデルなる考え方がある。 *4
また、分子が容器の内壁に衝突したり分子同士が衝突するという考え方はあるが、確かめられておらず、斥力によって衝突は回避されているかもしれない。 *5
一方、 Fig.13~14で示した結果は一意に定まらないが再現性があり、決してランダムな現象ではない。
ここから物理機能モデルは統計(確率)を用いず、再現性が担保された=決定論に立った解析に適応出来ると言える。
*3:量子力学で言われている不確定性原理、 "位置と運動量は同時に確定出来ない" と同じ意味合いと言える。
位置とは速度vの積分量であり、物質の変形量でもある。
運動量m・vを速度vで積分すれば 1/2 m・v2 = エネルギ(但し、これは速度エネルギ)である。
*4:量子力学では電子をスピンしながら運動するモデルとして表現しており、そのスピンの向きは定まらないものとして確率の概念を導入している。(アインシュタインは終生、これに異議を唱え、決定論の立場を取った)
但し、近年、スピンの向きを制御して揃える方法が確立され、量子コンピュータの原理に応用されている。
これは上記で圧縮操作を開始する時刻t=伸縮のタイミングを定めれば結果は再現性があると言う事と同じである。
また、Fig.17でブランコを始める際に復元力Fが最大となる斜面の頂上から始めれば漕ぐエネルギを節約できる=効率が良いのと同じである。
*5:電子同士はお互いに重ならない=パウリの排他原理
この詳細については既研究ノート パウリの排他原理のモデル化を参照されたい。
|
もくじへ戻る
 まとめ
まとめ
| ・ |
物理機能モデル手法を用いて気体分子をバネとして表現する事で以下の知見を得た。
|
| ・ |
固体、流体、気体の別無く、物質を見かけの体積が変化するバネと見なせば以下のエネルギを蓄える事が出来る。
・速度(運動)エネルギEv
・力(変形)エネルギEf
・熱エネルギEt
|
| ・ |
気体を圧縮膨張、過給除給する事はバネを伸縮させる事と等価であり、機械的に印加したエネルギが熱エネルギに変換される事で温度が変化するメカニズムを説明出来た。
|
| ・ |
物質を見かけの体積が変化するバネと見なす事は、アインシュタインの一般相対性理論、ド・ブロイの物質波と同じ見方である。
|
| ・ |
量子(電子)~固体物質~気体分子~熱力学上の現象まで通貫して表現する事が出来る。
|
| ・ |
統計(確率)を用いず再現性が担保された=決定論に立った解析に適応出来る。
|
もくじへ戻る
 脚注・参考文献
脚注・参考文献
脚注:
[1]:機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年 P15
参考文献:
・角田鎮男 ほか:製品開発のためのモデル化手法(展開と統合) 日本機械学会 [No.98 8]
機械力学・計測制御講演論文集 98.8.17 20 ・札幌 )
・機械の力学 長松昭男 著 朝倉書店刊 2007年
・複合領域シミュレーションのための電気・機械系の力学 長松昌男、長松昭男 共著 コロナ社刊 2013年
・次世代のものづくりのための電気・機械一体化モデル 長松昌男 著 共立出版刊 2015年
・機械学会交通物流部門 連続講習会No.12-5 資料
"機械ー電気の統合モデルによるモデルベース開発" 角田鎮男 著 2021年
"機械工学から見た相対性理論" 五十川晋一 著 2021年
・機械学会交通物流部門 連続講習会No.22-80 資料
"機械工学から見たブラックホール" 五十川晋一 著 2022年
・機械学会交通物流部門 連続講習会No.24-53 資料
"物質の柔性が粒子と波動性に及ぼす影響" 五十川晋一 著 2024年
・ホーキング、宇宙を語る―ビッグバンからブラックホールまで 林一訳 ハヤカワ文庫NF 1995年
・赤外吸収スペクトルと分子構造研究一バネと玉の振動から形を推測する 岡本裕巳 著 化学と教育 47巻1 号 1999 年
もくじへ戻る
 関連エッセイ:
関連エッセイ:
研究ノート 力学の双対性から見たプランクの公式の導出
研究ノート ブラックホールのエネルギ輻射のモデル化
研究ノート 電子レンジの物理モデル化
研究ノート パウリの排他原理のモデル化
研究ノート 力学の双対性から見た超伝導現象
研究ノート 非線形振動は捉えどころが無い?
研究ノート 浮遊する柔らかい物質の振動解析
研究ノート 重力発現モデル
研究ノート 光速に関する考察
研究ノート 物質破壊(崩壊)のモデル化
研究ノート 力学の双対性から見たプランク定数
研究ノート 電子の2重スリット実験に関する仮説
研究ノート ド・ブロイ波の力学的解釈
素粒子の質量はなぜ巾があるのか?
年頭所感:地球温暖化の仕組み
オーラの可視化
年頭所感:ランダムとは何か?
柔らかい力士とは?
二人のこころ模様
理性と感性の往来
年頭所感:ニュートンとフックはなぜ仲が悪かったのか?
相対性理論=双対性理論 愛とは何か?
年頭所感:双対ということ
無断転載は御遠慮願います。
ご質問、ご意見はこちらまで。
エッセイ目次に戻る
| 

























