Ev = 1/2 m・v2	Ev：速度（運動）エネルギ、m：質量、v：バネ端部速度	（1.1）
Ef = 1/2 H・f2	Ef：力（変形）エネルギ、H：柔性、f：バネ復元力	（1.2）
E = Ev + Ef = const.		（1.3）

上式は力学の双対性を現し、式（1.3）は対になったエネルギの和は常に一定となる事からエネルギ保存則と呼べる。
補足資料1参照

　次に、物質は絶対零度　0（k）＝（-273.15℃）以上で熱エネルギEtは以下のように定義される。

Et = m・Cp・T　　Et：熱エネルギ、m：質量、Cp：比熱、T：温度	（1.4）

熱エネルギEtは同じ内包量*²である力エネルギEfに変換出来るので、式（1.2）を変形して等価な力が求められる。
この力を最初にバネに印加しておくことで、物質が熱エネルギを蓄えて振動している事を力学的にバネの伸縮に置き換えて表現する事が出来る。詳細は 補足資料9参照

^*1：ド・ブロイの物質波と言え、物質全般はバネと見なす事が出来る。
*²：後述する

　プランク曲線は、放射される光のエネルギの振動数スペクトル（成分）が温度が高くなるほど振動数の高い方、すなわち赤色から青色を経て白色の方向に遷移する事を示している。
光を放射するという事は物質が振動していると言う事であり、振動数と物質が蓄えているエネルギの関係が温度に因って変化すると言う事である。
彼が研究していた黒体輻射とは、閉じ込められた溶鉱炉内で鉄が放つ光を観察する場合、窓の面積が限りなく小さい場合に外部からの光の侵入を無視出来る≒真っ暗闇という意味合いでこう呼んだものである。
音で言えば外の騒音を遮断した防音室内で、お寺の鐘の温度を振って叩いた時の周波数分析に相当する。
光の代わりに物質を振動させた時のエネルギを分析すると考えれば、この曲線を導出する事が出来そうである。
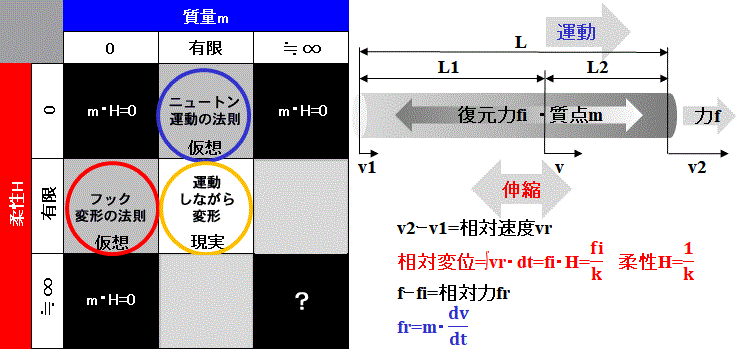
力学の双対性から見ると前述の様に以下の性質がある。

・エネルギは質量m、柔性Hに比例する。式（1.1）～（1.3）
・エネルギは温度Tに比例する。式（1.4）
・振動数fは物質の質量m、柔性Hに反比例する
・物質をn連のバネとして表すとn個に分割されたバネの質量m'と柔性H'は全体の1/nとなる。

　スペクトル分布は複雑な振動波形の中に、複数の振動数の正弦波形が含まれる寄与度を表していると言える。
溶鉱炉内の鉄を塊と見た場合、

・塊全体の質量mは鉄の原子1個の質量m'がアボガドロ数の整数倍=nモル個連なった複合質量と見なせる。
・塊全体の柔性Hは鉄の原子1個の柔性H'がアボガドロ数の整数倍=nモル個連なった複合柔性と見なせる。

　仮にその集合は均一とは限らないとすれば、例えば原子7、17、23個と言った小塊の集合を考える事が出来る。
これは一つの大陸上に存在する複数の国家の人口密度は均一では無いことに喩えられる。
鉄の塊が均一で無いならば、個々の質量m、及び柔性Hが異なる小塊の集合という見方が出来る。
塊全体が示す物理的性質は質量mや柔性Hが異なる小塊の分布（重ね合わせ）という見方が出来る。
この概念がスペクトル分布と言える。
エネルギについても同様に、原子の小集団=小塊が持つエネルギは原子1個が持つエネルギの整数倍になる。
この見方に基づき、本報の質量m、柔性Hをもった物質のモデル=バネを例えば1/2、1/3、1/4～1/nに分割していった場合、分割数に比例して増大する固有振動数がn個得られる。
物質の振動の源となる熱エネルギは式（1.4）で与えられるが、分割数をn、分割された質量をm'とした場合、温度Tを維持する為に印加しなければならない熱エネルギは、

Et = m'・Cp・T・n	（1.5）

　ここで留意すべきは、温度Tは連続値を取るが、nは整数、 質量m'、熱エネルギEtは離散値を取る少数である。
次に、本報の物質のモデル=バネでは1次元方向に伸縮するモデルであるから、現実の3次元の体積を持って伸縮する物質のエネルギを表現するには以下のようにnの3乗としなければならない。

Et = m'・Cp・T・ n3	（1.6）

　次に、質量m'が単純に1/n=等分割ならば、nは約分されてEtはTに比例するだけで分割数nの増加に対してスペクトル分布のようなピーク値を持つ事は出来ない。　Fig.3-1参照
そこで 等分割：y = 1 / x のような双曲線の反比例関係ではなく、x軸、y軸で交差するような直線反比例の関係を与える。
本報では、以下に示すような直線を仮定した。

・x軸：分割数n、y軸：分割された柔性H'とし、nの増加に伴い柔性H'を低下させる。

　ここで、等分割で無いのに整数nを掛けるのは奇異に思われるかもしれないが、熱エネルギEtは物質に印加すべきエネルギだが、それを蓄える物質の質量m' 、柔性H'は独立して任意の値を取り得るという事である。
こうする事により、分割数nと温度Tに応じて質量m' 、柔性H'が変化し、バネに蓄積されるエネルギは分割数nの増加に対してピーク値を持つことが出来る。　Fig.3-2参照
Fig.3-2は柔らかい物質のモデルを用い、環境温度50°（k）、物質温度500°（k）に於いて分割数nを1→60まで振った結果から、質量m' 、柔性H'、振動数f、エネルギEtをプロット（赤）したものである。
上段左図は分割数nと柔性H' 、上段中図は同、質量m'の反比例関係を示し、以下の式で表される。

n：分割数 = 1～60
n_Ini：分割数任意値 = 41、43、47、53 = 直線のx切片
H：物質全体の柔性 = 1.0e^-3 （ mN⁻¹ ）
m：物質全体の質量 = 0.1（Kg）
H'= f（n）：分割された柔性
m'= f（n）：分割された質量
T：温度（k） = 500、1000、1500、2000
b_rate = 1.0e⁻⁷　温度に対する柔性の変化率（mN⁻¹k⁻¹ ）（仮想の値である）
b = f（T）= H – b_rate・T　柔性=直線のy切片
a = f（T） = b / n_Ini 　直線の傾き
x = n　直線のx座標

H' = y = a・n =（H – b_rate・T）/ n_Ini・n 　直線のy座標	（1.7）

m'= H'/ H ・m	（1.8）

　原子1個=量子=素粒子の柔性H'は人為的に決める事は出来ないが、工学の分野ではバネの設計のように課題に応じて材質（元素）、線径、長さや巻き数を決めて柔性H = 1/K　K：バネ定数は任意に設定出来、その結果バネ自身の質量mも決まる。
式（1.7）（1.8）で温度Tと分割数nを振って物質の柔性H'、及び質量m' が決まるようにしたのはこれに倣ったものである。

なお、 本報ではx軸、y軸で交差するような直線反比例の関係を与えたが、双曲線のように等分割でなければどんな反比例関係でも良く、例えば乱数を用いた疑似ランダムな分割でも良い。　Fig.3-3参照
これは街中の騒音の周波数分析を例に取れば、サンプリングした音響エネルギに含まれる音源は音楽の様に人為的に整えたものでは無く、ランダムであるという事である。

　次に式（1.6）のm'に式（1.7）（1.8）を代入すると、温度T 、分割数nに従って質量m'が変化する際のバネに印加すべき熱エネルギEtは、

Et = H' / H ・m・Cp・T・n3 =（（H – b_rate・T）/ H ・n_Ini）・n・m・Cp・T・n3	（1.9）

H、m、p、b_rate、n_Ini、Cp は定数であり、熱エネルギEtを分割数nと温度Tの関数として表す事が出来る。
nを増加させて行くと式全体にn³が掛かっているが、（　）内は減少するので途中でピーク値を持つ。　Fig.3-2下段左図

一方、物質の自由振動における振動数fは以下で表され、質量m'、柔性H'と振動数fは反比例する。^*3

f = 1 /（2π √（m'H'））	（1.10）

^*3：E = h・ν　に於ける振動数νは物質の最小単位＝量子として見た時の振動数である事に注意。

m'、H'に式（1.7）（1.8）を代入すると、

f = 1 /（2π（H – b_rate・T）/ n_Ini・n・√（m / H））	（1.11）

熱エネルギEtと同じく、振動数fを分割数nと温度Tの関数として表す事が出来る。
分割数nの増加と共に分母の（　）内は減少し、振動数fは増加する。　 Fig.3-2上段右図
x軸：振動数f 、y軸：エネルギEtに取るとFig.3-2下段中図が得られる。

ここでエネルギの定義をあらためて以下に示す。

・エネルギEv_INT：物質＝鉄塊が蓄えている速度（運動）エネルギ＝式（1.1）
・エネルギEf_INT：物質＝鉄塊が蓄えている力（変形）エネルギ＝式（1.2）
・エネルギE_SUM_INT = Ev_INT + Ef_INT：物質＝鉄塊が蓄えている総エネルギ＝式（1.3）
・エネルギEt：物質＝鉄塊の温度を維持する為に必要な熱エネルギ＝溶鉱炉に供給すべきエネルギ＝式（1.4）
・エネルギEr = Ev_INT：物質＝鉄塊から放射されるエネルギ＝速度（運動）エネルギ＝式（1.1）
・広義には振動する空間から放射されるエネルギには電磁波と重力波がある。
・空間とは実体の有無を問わない。　例：天体は実体が有る。　天体間は実体が無い。

ここで電磁波と重力波について説明するが、力学と電磁気学の相似則により以下の相似関係にある。

・電磁波：電気のLC共振回路から発生する電場の磁場の周期的な変動に伴う実体の無い空間の歪みの伝播。
・重力波：物質の伸縮により発生する重力場とバネ場の周期的な変動に伴う実体の無い空間の歪みの伝播。

光は電磁波の一種であるが、本報のモデルは実体のある柔らかい物質の伸縮なので重力波に相当する。
実体の無い空間の歪みの伝播エネルギは外延量と呼ばれる以下のエネルギである。

・電磁波：電場の周期的な変動に因る静電エネルギ
・重力波：重力場の周期的な変動に因る速度エネルギ

なお、力学的に空間に外部から直接作用出来るのは電位差や速度差のような外延量であり、これに曝される空間内部には内包量と呼ばれる以下のエネルギが生じる。

・電磁波：磁場の周期的な変動に因る電磁エネルギ（電磁波はコイルに生じる磁束で検出される）
・重力波：バネ場の周期的な変動に因る力エネルギ（重力波は空間の歪み＝変位で検出される）

これらをまとめたのが、表1である。補足資料10にも説明あり。
注：実体の有る空間＝物質、実体の無い空間＝量子力学や電磁気学で言われる真空を意味する。

表1

力学

電磁気学

空間

実体有り 運動 速度v 質量m 速度エネルギ ニュートン 　 変形 復元力F 柔性H 力エネルギ フック 　 物質波　ド・ブロイ 実体無し 重力場 速度v 質量m 速度エネルギ ニュートン 　 バネ場 復元力F 柔性H 力エネルギ フック 　 重力波　アインシュタイン 電場 電圧V 静電容量C 静電エネルギ ｱﾝﾍﾟｱ ﾏｯｸｽｳｪﾙ 磁場 電流I ｲﾝﾀﾞｸﾀﾝｽL 電磁エネルギ ファラデー 　 電磁波　マックスウェル

量子力学

近接作用

万有引力（ニュートン）

クーロン力（クーロン）

　Fig.3-1～3に分割数nを振った時の柔性H'、質量m'、振動数f、供給すべき熱エネルギEtの変化を示す

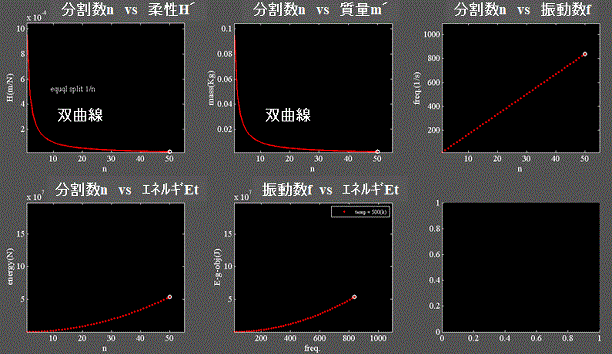
Fig.3ｰ1 ・上段左、中：分割数nに対して質量m' 、柔性H'を等分割する場合、 ・下段左、中：エネルギEtはスペクトル分布のようなピーク値を持つ事は出来ない。 ・白プロットはエネルギEtがピークとなる時の座標を示す。

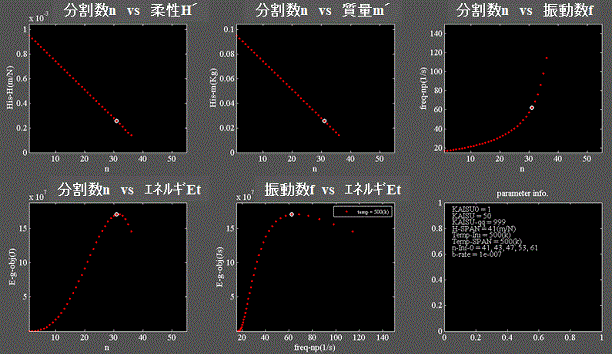
Fig.3-2 ・上段左、中：分割数nに対して質量m' 、柔性H'を等分割にしない場合、 ・下段左、中：エネルギEtはピーク値を持つ事が出来る。 ・白プロットはエネルギEtがピークとなる時の座標を示す。

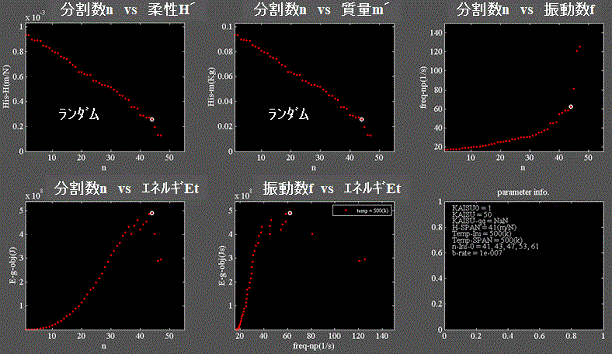
Fig.3-3 ・上段左、中：分割数nに対して質量m'、柔性H'を乱数を用いて疑似ランダムに分割した例である。 ・下段左、中：エネルギEtはピーク値を持つ事が出来る。 ・白プロットはエネルギEtがピークとなる時の座標を示す。

Fig.4に分割数nを振った時の柔らかい物質のモデルから放射されるエネルギErの観測結果を示す。

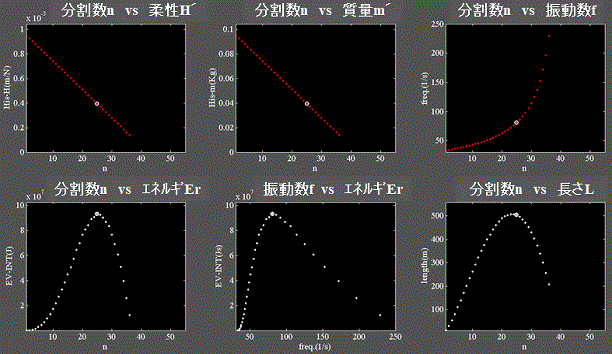
Fig.4 ・上段のフォーマットはFig.3-2と同じである。 ・下段左：x軸：分割数n、y軸：放射エネルギEr。 ・下段中：x軸：振動数f、y軸：放射エネルギEr。この曲線（本報では便宜上曲線Aと呼ぶ）は振動する物質から放射されるエネルギと振動数の関係を表す。 ・下段右：参考にx軸：振動数f、y軸：伸縮しているバネ=物質の長さL（最大値）に取ったもの。

　一方、曲線Aはy軸は体積で除していないので単位は（Js）としている点が異なる。Fig.5右図参照
これは柔らかい物質のモデルは伸縮しているので体積が定まらない=密度が定まらないからである。
本報の物理機能モデルとは冒頭のFig.1で示したように、物質内を質点が移動する=密度が不均一である性質が表現されている事に留意されたい。

Fig.5

　両曲線は似ているが、曲線Aは分割数nと温度Tの関数である式（1.9）を由来としている点に注意。
又、前述のように物質の振動の原資となる熱エネルギは3次元としたが、バネ自身は1次元のエネルギである点に注意。
従って、x、y、zの3軸方向に伸縮する物体の体積変化は1軸方向の変位の3乗になるので、変位にまつわる物理量、力F、速度vは3次と考えなければならない。 ここで便宜上、エネルギをサフィックス3を付けて表すと、

Et3 = Ef3 = 1 / 2H'・F6	（1.12）

力Fは√Tに比例するのでTで表すと、

Ef3 = 1 / 2H'・T3	（1.13）

H'に式（1.7）を代入して、

Ef3 = 1/2（H – b_rate・T）/ n_Ini・n・T3	（1.14）

同様に速度エネルギは

Ev3 = 1/2m'・ T3	（1.15）

m'に式（1.8）を代入して

Ev3 = 1/2（H – b_rate）・T /（H ・n_Ini）・n ・m・T3	（1.16）

E3 = Ev3 + Ef3 = （H・T3 – b_rate・T4）/ n_Ini・n・（1＋m）	（1.17）

このように、3次元の柔らかい物質が蓄えるエネルギは温度Tの4次関数で表す事が出来る。
これは黒体から放出される輻射エネルギ密度はシュテファンボルツマンの法則では温度Tの4乗に比例する事と符合する。
なお、振動数に関しては質量m、柔性Hのみに依存するので次元は変わらない。

1.分割された柔性H'は分割数nに反比例し、振動数は比例する。
2.物質に蓄えられる熱エネルギは式（1.6）から分割数n、及び温度Tに比例する。

　温度上昇に伴いスペクトルが高エネルギ密度側に遷移するのは上記2.によるものである。
一方、温度上昇に伴いエネルギのピークが高振動数側に遷移するには振動数がオフセットする仕組みが必要と考え、次の仮説を立てた。

・温度Tの上昇に伴い原子1個の柔性H'は低下する＝温度Tに反比例して硬化する。

　一般的には鉄に限らず物質は温度上昇と共に軟化するものだが、本報のモデルでは温度Tの上昇＝熱エネルギEtの増加はバネの振幅を増大させるので、外部から観測すればバネ長が伸びた＝軟化したように見える。 ⁴
これは式（1.3）をエネルギの比率で見ると、柔性H'が低下すれば力エネルギEfは減少するが、増加した熱エネルギEtは速度エネルギEvを増大させると解釈される。
ド・ブロイが示したように万物は粒子と波動の性質を持つが、温度の上昇に伴い波動より粒子の性質が顕著になるという仮説でもある。
この仮説を用いて物質温度Tを4水準に振った結果をFig.6に示す。
ここには温度上昇に伴い、曲線Aがプランク曲線の様に高振動数側、及び高エネルギ側に遷移している様相が現れている。

⁴：タンパク質はアミノ酸分子が鎖状に繋がったものだが、温度が上昇すると凝固するが、中には上昇が続くと再び軟化するという性質を持ったものがある。
これはアミノ酸分子の配列によって粒子の性質が顕著になるか波動の性質が顕著になるかが決まると考えられる。

Fig.6 ・温度上昇に伴い柔性が低下＝硬化する仕組みは上段左図に於ける直線（赤→水色）のy切片に示される。 ・4点の白プロットは各温度に於いてスペクトル（放射エネルギEr）がピークとなる時の座標を示す。 ・上段左：分割数n vs 柔性H' ・上段中：分割数n vs 質量m' ・上段右：分割数n vs 周波数 ・下段左：分割数n vs 放射エネルギEr ・下段中：振動数 vs 放射エネルギEr ・下段右：分割数n vs 長さ　温度の上昇と共に物質長さLは放射エネルギと同様に増加=伸びる事が判る。

U(ν)dν = 8πkβ/c³・1/(e^(βν/T) − 1)・ν³dν

U：エネルギ密度、 k:ボルツマン定数、 β：実験値から同定する値、 kβ=h：プランク定数、c：光速、T：温度 、ν：振動数

　この式は直接、振動数νとエネルギ密度Uの関係を示しており、エネルギを振動数によって分割したと言う意味である。
8πkβ / c³ は定数ゆえ2番目の 1/(e^(βν/T) − 1) の項がエネルギ密度Uの大小を左右し、νの増加に反比例して減少する。
一方、全体はνの3乗が掛かっているのでνの増加に伴いUはピーク値を持つことになる。
この2番目の項の役割は本報に於いてエネルギを等分割にしない為の処置と言える。
そして2番目の項の分母に於けるeのべき乗 βν/T = 2.82 の時にのみ、Uはピーク値を持つ事が知られている。
これは物理的ではなく、数学的な性質と言える。
プランクは当初、βは実験値から同定される値としていたが、振動数νと温度Tは互いに独立ではなく、その比率は常に一定=定数になる事を認識したと思われ、これは物理的解釈に到達したと言えよう。
ここから既知のボルツマン定数k、及び β = 2.82 T/ν の関係を用いて算出した新たな定数をh：プランク定数としている。

　一方、本報では式（1.10）に示すように振動数fは柔性H'と反比例の関係にあるので、プランクの公式からもν/Tが1を超えて増加してゆく為には柔性H'と温度Tは反比例の関係でなければならない事が判る。
筆者はその比率 H' / T = b_rate = 1.0e⁻⁷ としているが、この値を増減させてみると曲線Aが温度上昇に伴い、高振動数側に遷移する様が現れるには適切な範囲が存在する事が判った。

　プランクは物質の柔性については言及していないが、力学の双対性に基づく物理機能モデルでは物質をバネとして表すので、バネをn分割すると柔性H'は質量m'と共に整数比で減少し、式（1.1）、（1.2）に示したように蓄えられるエネルギも同様である。
結果として分割された個々の物質の固有振動数とエネルギの対が決まる。
従って、本報ではスペクトル分布のように様に振動数についてエネルギを分割するという発想ではなく、物質そのものを分割すれば、結果として振動数とエネルギの関係はスペクトル分布のようにピーク値を持つことになる。
先に本報の柔らかい物質のモデルは伸縮して体積が定まらないゆえに曲線Aのy軸は物質の体積で除していないと述べた。
これは万物は柔性Hと質量mなる物理特性を対で持つと言う見方に由来する。
これが力学の双対性であり、エネルギ保存則と呼べる理由である。　補足資料1参照
ここであらためてプランクの公式の導出、及びプランク定数について筆者が立てた二つの仮説を以下に示す。

1.原子1個の柔性Hは温度Tに反比例する。（高温では硬化する）
2.原子1個の柔性Hは原子量に反比例する。　既研究ノート　力学の双対性から見たプランク定数より

なお、プランクの公式に物質の元素に関する値が含まれないのは上記仮説の2.で説明出来る。

　プランクはこの公式を1900年に提示したが、その後1905年に光電効果を説明する為の光量子仮説、更に1916年に一般相対性理論を提示したアインシュタイン、そして1924年に物質波なる概念を提示したド・ブロイも柔性、又は剛性という物理特性には言及していない。

・ボルツマン定数k：元素に因らない熱エネルギEtと温度Tの関係を示す。
・プランク定数h ：元素に因らない光エネルギErと振動数νの関係を示す。

プランクは以下を結び付けようとしていたものと思われる。

・熱エネルギと光エネルギとの関係。
・温度Tと振動数νの関係。

本報では力学の双対性に基づくエネルギ保存則から以下を出発点にしている。

・元素に因らない温度TとエネルギEの比例関係　式（1.5）
・元素に因らない柔性Hと振動数fとの反比例関係　式（1.10）

kβ=h から逆算される β= 4.7992e^-11 は温度Tと振動数νを関連付ける定数という見方が出来るが、本報の式（1.11）に於けるb_rateに相当すると考えられる。

先に電磁波と重力波の関係を示したが、エネルギの中で熱エネルギEtと光エネルギErは以下の表2に示す関係にある。

表2

力学エネルギE	速疎（運動）エネルギEv 力（変形）エネルギEf 熱エネルギEt	外延量 内包量
光電エネルギE	静電エネルギEC 光エネルギEr 電磁エネルギEL	外延量 内包量

　表2は熱エネルギEtと光エネルギErは互いに内包量と外延量の関係にある事を示している。
これは溶鉱炉内の温度を保つために必要な熱エネルギEtは原因、放射される光エネルギErは結果という事になる。
このような見方をするとボルツマン定数kに遅れてプランク定数hが提示された事により、力学上の因果関係が明らかになったと言える。
また、アインシュタインが説明した光電効果や太陽光に因って物質が温められる効果は光エネルギErが原因で熱エネルギEtが結果と言う事になる。
つまり熱エネルギEtと光エネルギErはお互いに因果関係が双方向になっている。
速度vと力F、電圧Vと電流Iが双対の関係にあるゆえに、エネルギについても双対性が成り立つのである。

　エネルギについては、熱、流体、材料、機械、機構、電磁気、量子等の諸力学において個別に定義されている。
これは産業革命以降、様々な分野の現場で遭遇する現象について後追いで理論付けがなされて来た成果と言える。
しかしながら、現場で起こる課題の解決にはエネルギという視点は必ずしも必須だったという訳では無く、力や速度、圧力、体積、流量、温度といった物理量を用いた種々の法則、例えば、ニュートン、フックの法則、ボイル・シャルルの法則に倣う事で済んでいたと言う見方が出来る。
力学の双対性とは、前述の様にエネルギ保存則と言っても良い。
プランクの公式にボルツマン定数を組み込んだのは、エネルギ保存則という視点があったのではないかと思われる。
また、ボルツマンとプランクはピアノを演奏するという共通点がある。
音楽に於ける音階にはオクターブ（振動数2倍）の間を12分割^*4　するという平均律なる理論があり、ピアノの調律もこれを基準としている。
二人は音楽が旋律を奏でるという事は音のエネルギが時系列的に2^1/12 の比率で飛び飛びに変化してゆく現象である事を認識していたと思われる。
ピアノの鍵盤の並びを見れば、音楽は量子的な振る舞いをするという見方が出来、黒体輻射の研究過程で少なからずヒントになったのではないかと思われる。

^*4：中東、アジア圏には更に細かい分割～微分音と呼ばれるものがある。