|
Last update : 2001.07/21
大和の船型に関する一考察
|
|
問題の提起。 
 大和(WWIIの方。為念)の船型について推進抵抗の観点から記述された文章は
数多く存在しますが、球状艦首の採用による最大速力27kt附近での抵抗減少に
スポットが当てられることが多く、船型決定の際に何が最も考慮されたか、
最も重視した速力域はどのあたりであり、逆に他のどの速力域での性能は
重視されなかったのか、
という点についての説明はあまり多くありません。
(私が知らないだけかもしれませんが...。)
大和(WWIIの方。為念)の船型について推進抵抗の観点から記述された文章は
数多く存在しますが、球状艦首の採用による最大速力27kt附近での抵抗減少に
スポットが当てられることが多く、船型決定の際に何が最も考慮されたか、
最も重視した速力域はどのあたりであり、逆に他のどの速力域での性能は
重視されなかったのか、
という点についての説明はあまり多くありません。
(私が知らないだけかもしれませんが...。) というわけで微力を尽くして計算をしてみた結果、
「大和の船型の決定にあたっては、最大速力である27kt附近での抵抗減少が
最重要視されており、逆に基準速力の16kt附近はあまり重視されていなかっ
たのではないか?」という仮説に到達してしまいました。
というわけで微力を尽くして計算をしてみた結果、
「大和の船型の決定にあたっては、最大速力である27kt附近での抵抗減少が
最重要視されており、逆に基準速力の16kt附近はあまり重視されていなかっ
たのではないか?」という仮説に到達してしまいました。 以下にその内容を述べたいと思います。
以下にその内容を述べたいと思います。
理論。

 本駄文をお読み頂く上で必要であろう知識を、
簡単にまとめてみます。
本駄文をお読み頂く上で必要であろう知識を、
簡単にまとめてみます。・ 船体の全抵抗は、 摩擦抵抗と剰余抵抗とに分割することができる。  摩擦抵抗とは文字どおり船体表面と水との摩擦による抵抗です。
剰余抵抗は全抵抗から摩擦抵抗を差っ引いた分であることからこの名がありますが、
船体が水面に波を起こすことによる造波抵抗、水中に渦を起こすことによる造渦抵抗、
などを含むとされています。
摩擦抵抗とは文字どおり船体表面と水との摩擦による抵抗です。
剰余抵抗は全抵抗から摩擦抵抗を差っ引いた分であることからこの名がありますが、
船体が水面に波を起こすことによる造波抵抗、水中に渦を起こすことによる造渦抵抗、
などを含むとされています。 ここで、全抵抗:Rt、摩擦抵抗:Rf、
剰余抵抗:Rrと置き、
式の形で表わすならば、
ここで、全抵抗:Rt、摩擦抵抗:Rf、
剰余抵抗:Rrと置き、
式の形で表わすならば、  Rt = Rf +
Rr ...(1)
Rt = Rf +
Rr ...(1)となります。また、 有効馬力:EHPと抵抗:R、速力V との関係は
  EHPt = EHPf
+ EHPr
EHPt = EHPf
+ EHPrも成り立ちます。(有効馬力については こちらを参照して下さい...。)
計算。

1) 水槽試験結果  さてはて本題です。
さてはて本題です。 大和の推進抵抗については、「戦艦大和 その生涯の技術報告」の
101頁に、A140-F5(最終案の1つ前)の水槽試験の結果
が掲載されています。
大和の推進抵抗については、「戦艦大和 その生涯の技術報告」の
101頁に、A140-F5(最終案の1つ前)の水槽試験の結果
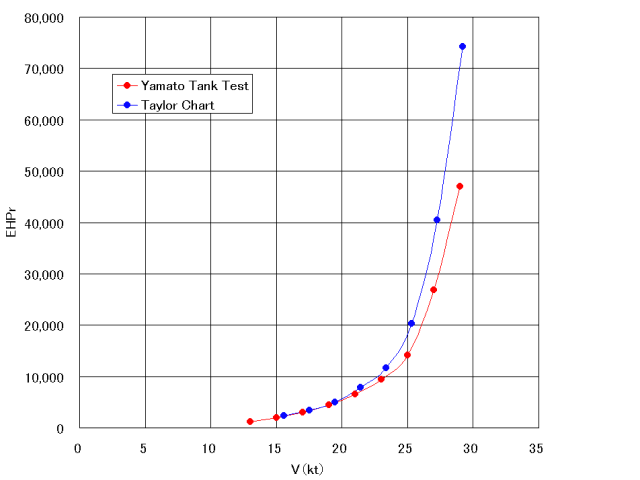
が掲載されています。Table1. A140-F5 (Model No. 1029B) Tank Test Result
 上の表の見方ですが、「27ktにおける全有効馬力は60750HP、うち摩擦抵抗によるもの
33967HP、剰余抵抗によるもの26783HP、剰余抵抗による有効馬力が全有効馬力に占める
割合は0.441」て感じです。
上の表の見方ですが、「27ktにおける全有効馬力は60750HP、うち摩擦抵抗によるもの
33967HP、剰余抵抗によるもの26783HP、剰余抵抗による有効馬力が全有効馬力に占める
割合は0.441」て感じです。2) Taylor Chart  大和との比較を行うため、Taylor Chartを用いて大和と同大の船舶の剰余抵抗を
計算しました。
大和との比較を行うため、Taylor Chartを用いて大和と同大の船舶の剰余抵抗を
計算しました。 D.W.Taylorは米海軍の水槽の責任者を勤めた人物で、彼は1910年頃に巡洋艦型船尾を
有し軍艦に適した標準船型について、系統だった模型試験を行いました。試験結果を
取りまとめた図表は「Taylor Chart」と呼ばれ、長く艦船の抵抗と所要馬力の
見積もりに使用されています。
D.W.Taylorは米海軍の水槽の責任者を勤めた人物で、彼は1910年頃に巡洋艦型船尾を
有し軍艦に適した標準船型について、系統だった模型試験を行いました。試験結果を
取りまとめた図表は「Taylor Chart」と呼ばれ、長く艦船の抵抗と所要馬力の
見積もりに使用されています。 計算に使用したのは「造船設計便覧」第3編に掲載されているTaylor水槽の図表です。
(厳密に言うとこれはTaylorの図表そのものではなく、Taylorの試験結果を
Schoenherrの摩擦抵抗式によって再解析したものなそうですが、結果が出るから
良しとしましょうか。)
計算に使用したのは「造船設計便覧」第3編に掲載されているTaylor水槽の図表です。
(厳密に言うとこれはTaylorの図表そのものではなく、Taylorの試験結果を
Schoenherrの摩擦抵抗式によって再解析したものなそうですが、結果が出るから
良しとしましょうか。) 使用した図表では、幅吃水比 B/d、柱型係数 Cp、
排水量長さ比 ▽/L3、フルード数 V/(gL)1/2
の値により、剰余抵抗係数Crが与えられます。
使用した図表では、幅吃水比 B/d、柱型係数 Cp、
排水量長さ比 ▽/L3、フルード数 V/(gL)1/2
の値により、剰余抵抗係数Crが与えられます。
 大和のこれら数値を、
大和のこれら数値を、
Table2. 剰余抵抗係数Cr(Taylor水槽の図表)
 この表の見方ですが、「Cp=0.65、▽/L3=0.004、
B/d=3.00のとき、V/(gL)1/2=0.16での剰余抵抗係数
Crは0.52」
といった感じです。
この表の見方ですが、「Cp=0.65、▽/L3=0.004、
B/d=3.00のとき、V/(gL)1/2=0.16での剰余抵抗係数
Crは0.52」
といった感じです。 フルード数 V/(gL)1/2=0.16(即ち15.58kt、8.02(m/sec)です)における、
剰余抵抗による有効馬力 EHPrについての計算例を
以下に示します。
フルード数 V/(gL)1/2=0.16(即ち15.58kt、8.02(m/sec)です)における、
剰余抵抗による有効馬力 EHPrについての計算例を
以下に示します。 大和のB/dは3.548ですから、
B/d=3.00でのCrは0.52、B/d=3.75での
Crが0.64ということで一次の補間を行い、
Cr
は0.608ということにします。
大和のB/dは3.548ですから、
B/d=3.00でのCrは0.52、B/d=3.75での
Crが0.64ということで一次の補間を行い、
Cr
は0.608ということにします。 で、例によって例の式
で、例によって例の式
 剰余抵抗 Rr = 21999(kgf)
剰余抵抗 Rr = 21999(kgf)を得ます。  例によって例の式
例によって例の式
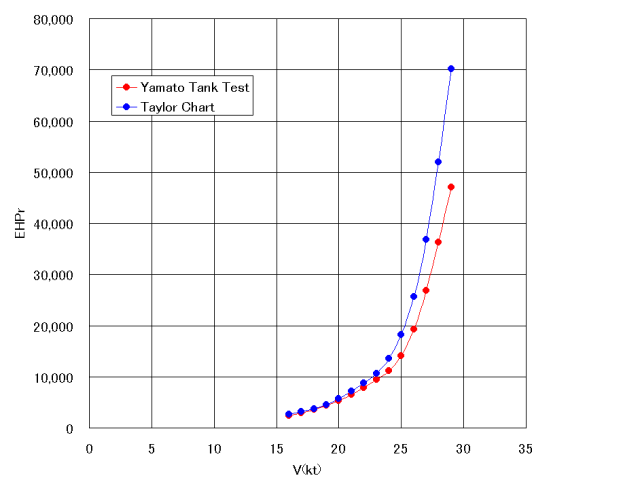 Figure2. 補間の結果  というわけで同速力での剰余抵抗による有効馬力がわかりましたので、
両者を比較してみます。
というわけで同速力での剰余抵抗による有効馬力がわかりましたので、
両者を比較してみます。 水槽試験結果とTaylor Chartによる計算結果の「比」を
水槽試験結果とTaylor Chartによる計算結果の「比」を
 計算により得られた結果を、以下の表と図に示します。
計算により得られた結果を、以下の表と図に示します。Table5. 水槽試験の結果とTaylor Chartによる計算結果の比較(2)
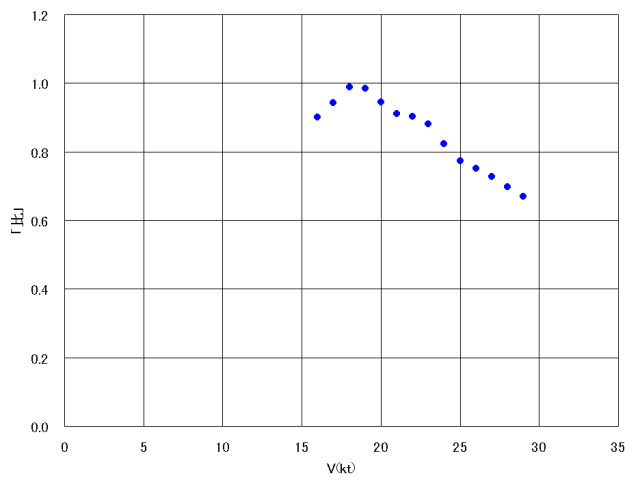 Figure3. 水槽試験の結果とTaylor Chartによる計算結果の比較(2)  このグラフからは、以下の点が読み取れます。
このグラフからは、以下の点が読み取れます。(1)大和の船型は16kt〜29ktの速力域のほぼ全てにわたり、Taylorの標準船型よりも 剰余抵抗が少ない。 (2)大和の船型とTaylorの標準船型を比較した場合、 大和は特に高速域における剰余抵抗が少ないが、 逆に低速域での剰余抵抗の減少はそれほどではない。 (3)大和の船型とTaylorの標準船型を比較した場合、大和の船型では 全速力の27kt附近では27%程度は剰余抵抗による有効馬力が減少しているが、 基準速力の16kt附近では剰余抵抗による有効馬力は 10%程しか減少していない。また18kt附近では両者にほとんど差がない。
結論。

 上記により本稿の結論を申し上げます。
上記により本稿の結論を申し上げます。(1)大和の船型とTaylorの標準船型を比較した結果、 大和では全速力附近で剰余抵抗が少なく、 逆に基準速力附近ではそれほどの差がなかった。 (2)よって、大和の船型の決定にあたっては全速力での 剰余抵抗軽減に意が用いられ、それに比べると基準速力での剰余抵抗の 軽減は軽視された可能性がある。  高速域での剰余抵抗の減少を図るのは推進抵抗の理論からも
常道かと思います。
高速域での剰余抵抗の減少を図るのは推進抵抗の理論からも
常道かと思います。 先に示したTable1.でも、16ktで剰余抵抗が全抵抗に占める割合は23%台であるのに
対し、27ktでのその割合は44%となっています
先に示したTable1.でも、16ktで剰余抵抗が全抵抗に占める割合は23%台であるのに
対し、27ktでのその割合は44%となっています つまり、剰余抵抗の削減による全抵抗の減少の効果は高速域ほど大きいのが
常識なので、高速域での剰余抵抗の削減に注力するのは
ある意味当然ではあります。
つまり、剰余抵抗の削減による全抵抗の減少の効果は高速域ほど大きいのが
常識なので、高速域での剰余抵抗の削減に注力するのは
ある意味当然ではあります。 その当然の結果が出たということで、ま、良かった良かったと言って
本稿を終了します。
その当然の結果が出たということで、ま、良かった良かったと言って
本稿を終了します。 ここまで長々とお付き合い下さった方、
ありがとうございました。
ここまで長々とお付き合い下さった方、
ありがとうございました。 ご批評ご感想など頂けましたら幸いです。
ご批評ご感想など頂けましたら幸いです。
主要参考文献

 「日本海軍全艦艇史 資料篇」 福井静夫 編集/KKベストセラーズ
「日本海軍全艦艇史 資料篇」 福井静夫 編集/KKベストセラーズ 「昭和造船史」(1巻) 日本造船学会 編/原書房
「昭和造船史」(1巻) 日本造船学会 編/原書房 「軍艦基本計画資料」 福田啓二 著/今日の話題社
「軍艦基本計画資料」 福田啓二 著/今日の話題社 「戦艦大和 その生涯の技術報告」 松本喜太郎 著/再建社
「戦艦大和 その生涯の技術報告」 松本喜太郎 著/再建社 「造船設計便覧」 関西造船協会 編
「造船設計便覧」 関西造船協会 編 「算法通論」 東京大学出版会
「算法通論」 東京大学出版会 本文章は上記図書を参考に藤原梟介の責任において記述してあります。
本文章は上記図書を参考に藤原梟介の責任において記述してあります。 どこかしらに間違いがあることを確信しておりますので、
参考になさる際には上記文献をあたられることをお勧めします。
どこかしらに間違いがあることを確信しておりますので、
参考になさる際には上記文献をあたられることをお勧めします。 論理的な批判・批評は喜んでお受けいたします(つーか嬉しいんですが)ので、
ご遠慮なくどうぞ。
論理的な批判・批評は喜んでお受けいたします(つーか嬉しいんですが)ので、
ご遠慮なくどうぞ。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||